
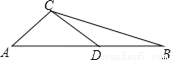
��ͼ���ڡ�ABC�У�AC=DC=DB����ACD=100�㣬���B�Ķ�����
 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧģ���Ծ� ���ͣ������
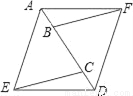
��ͼ����A��B��C��D��һ��ֱ���ϣ���ABF�ա�DCE�����ܵó���Щ���ۣ�����д���������ϵĽ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ�����꼶12���¿���ѧ�Ծ� ���ͣ������
ij�ص�һ����ɫ�߲�,���г�����ֱ������,ÿ������Ϊ1000Ԫ,���ּӹ�������,ÿ������4000Ԫ,�����ӹ�������, ÿ������Ϊ7000Ԫ.����һ�ҹ�˾���������߲�140��,�ù�˾�ӹ���������������:������߲˽��дּӹ�,ÿ��ɼӹ�16��, ������߲˽��о��ӹ�,ÿ��ɼӹ�6��,��ÿ�����ַ�ʽ����ͬʱ����.�ܼ��ڵ�����������,������15��ʱ�佫�����߲�ȫ�����ۻ�ӹ����.Ϊ��,��˾���������ַ���:
����1:���߲�ȫ�����дּӹ�;
����2:�����ܵض��߲˽��о��ӹ�,û���ü��ӹ����߲�,���г���ֱ�ӳ���;
����3:��һ�����߲˽��о��ӹ�, �����߲˽��дּӹ�,���պ�15�����.
������ǹ�˾����,���ѡ����һ�ַ���? ��ͨ������˵��.
ѡ����. �����������������������1���ͷ�����2���Ļ��������ֱ����������������辫�ӹ�x�죬��ּӹ�(15��x)�죬���ݾ��ӹ��������ּӹ�������140�г����̣��ⷽ��������ӹ��ʹּӹ��������죬�Ӷ����������Ȼ��ȽϿɵó��𰸣� ��������� �������� ����һ������Ԫ�� ������������Ԫ�� ����������x����о��ӹ�����15��x������дּӹ��� �� ���...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ�����꼶12���¿���ѧ�Ծ� ���ͣ���ѡ��
һ��������������20h��ɣ��ҵ�����12h��ɣ��ּ�����4h���Ҽ���ͼ�һ��������Ҫ��Сʱ��ɣ����軹Ҫx h��ɣ�����������з���Ϊ��������
A. 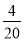 ��
��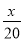 ��
��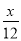 =1 B.
=1 B. 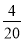 ��
��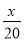 +
+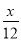 =1 C.
=1 C. 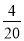 +
+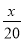 ��
��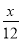 =1 D.
=1 D. 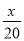 +
+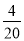 +
+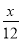 =1
=1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ�����꼶12���¿���ѧ�Ծ� ���ͣ���ѡ��
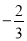 �ĵ����ǣ� ��
�ĵ����ǣ� ��
A. 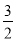 B.
B. 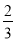 C.
C. 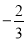 D.
D. 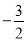
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�п���ѧģ���Ծ� ���ͣ������
�ֽ���ʽ��mn2��6mn+9m=_____��
m��n��3��2 ��������mn2��6mn+9m ��m��n2-6n+9�� =m��n-3��²�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�п���ѧģ���Ծ� ���ͣ���ѡ��
����ABC��AB���ϵĸߣ����л�������ȷ���ǣ�������
A. 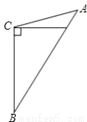 B.
B. 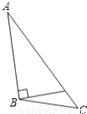 C.
C. 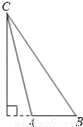 D.
D. 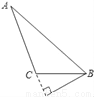
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʦ�����п���ѧ��ģ�Ծ� ���ͣ������
��ͼ����֪��ABC����C=90�㣮���ó߹���һ�������Σ�ʹCΪ�����ε�һ�����ǣ�������������ֱ���AB��BC��AC���ϣ���������ͼ�ۼ�����д������
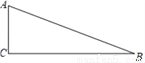
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�人���п���ѧģ���Ծ� ���ͣ������
��ͼ����DΪ��O��һ�㣬��C��ֱ��BA���ӳ����ϣ��ҡ�CDA=��CBD����1���ж�ֱ��CD�͡�O��λ�ù�ϵ����˵�����ɣ�
��2������B����O������BE��ֱ��CD�ڵ�E����AC=2����O�İ뾶��3�����BEC������ֵ��
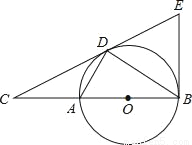
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com