练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    中， ， ， ，那么等于（ ）．

    A. B. C. D.

    A 【解析】∵，∴． ∵ ∴ 解得． ∵， ∴． 故选A.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：安徽省2018届九年级上学期第二次月考数学试卷 题型：解答题

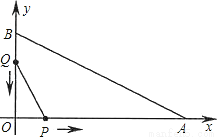
    如图，在平面直角坐标系中，已知OA=12厘米，OB=6厘米．点P从点O开始沿OA边向点A以1厘米/秒的速度移动；点Q从点B开始沿BO边向点O以1厘米/秒的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间（0≤t≤6），那么，当t为何值时，△POQ与△AOB相似？

    当t=4或t=2时，△POQ与△AOB相似． 【解析】试题分析：根据题意可知：OQ=6-t，OP=t，然后分和两种情况分别求出t的值． 试题解析：【解析】 ①若△POQ∽△AOB时，=，即=， 整理得：12﹣2t=t， 解得：t=4． ②若△POQ∽△BOA时，=，即=， 整理得：6﹣t=2t， 解得：t=2． ∵0≤t≤6， ∴t=4和t=...

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型：单选题

    如图，矩形ABCD的边平行于坐标轴，对角线BD经过坐标原点，点C在反比例函数y=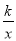的图象上．若点A的坐标为（﹣2，﹣2），则k=（　　）

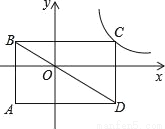
    A. 2 B. 4 C. 8 D. 16

    B 【解析】如图， ∵四边形ABCD为矩形，其边平行于坐标轴，对角线BD经过坐标原点O， ∴S△ABD=S△CDB，四边形BFOG和四边形EDHO都是矩形， ∴S△OBF=S△OGB，S△OED=S△ODH， ∴S△ABD- S△OBF-S△OED =S△CDB-S△OGB-S△ODH，即S矩形AEOF=S矩形CHOG， ∵点A的坐标为：（﹣2，﹣2）， ...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型：填空题

    二次函数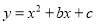，若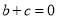，则它的图像一定过点__________．

    （1，1） 【解析】当时， ， ∴， ∵， ∴， 则． ∴一定过（1，1）点．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型：单选题

    如图，一次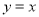函数与二次函数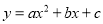图象相交于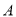、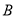两点，则函数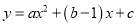的图象可能是（ ）．

    A. B. C. D.

    B 【解析】∵一次函数y=x与二次函数y=ax2+bx+c图象相交于A、B两点， ∴方程ax2+（b-1）x+c=0有两个不相等的根， ∴函数y=ax2+（b-1）x+c与x轴有两个交点， ∵二次函数图象与y轴的交点在正半轴上， ∴c＞0， ∴函数y=ax2+（b-1）x+c的图象与y轴的交点在正半轴上. 4个选项只有选项B符合条件，故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017年内蒙古乌兰察布市中考数学一模试卷 题型：解答题

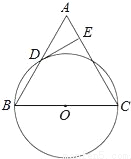
    已知：如图，在△ABC中，BC=AC，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E．

    （1）求证：点D是AB的中点；

    （2）判断DE与⊙O的位置关系，并证明你的结论；

    （3）若⊙O的直径为18，cosB=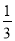，求DE的长．

    （1）证明见解析；（2）DE是⊙O的切线，证明见解析；（3）DE= ． 【解析】（1）证明：连接AD ∵AB为半圆O的直径, ∴AD⊥BC ∵AB=AC ∴点D是BC的中点 (2)【解析】 相切 连接OD ∵BD=CD，OA=OB， ∴OD∥AC ∵DE⊥AC ∴DE⊥OD ∴DE与⊙O相切 （3） ∵AB为半圆O的直...

    查看答案和解析>>

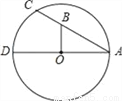
    科目：初中数学 来源：2017年内蒙古乌兰察布市中考数学一模试卷 题型：填空题

    如图，AD和AC分别是⊙O的直径和弦，且∠CAD=30°，OB⊥AD，交AC于点B，若OB=3，则BC=__．

    3 【解析】连接DC，则°，在三角形AOB中，AB=6，A0=,则CD=,AD=, AC=,BC=9-6=3

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省徐州市中考数学模拟试卷（2） 题型：解答题

    （14分）如图，在平面直角坐标系中，抛物线y=mx2﹣8mx+4m+2（m＞2）与y轴的交点为A，与x轴的交点分别为B（x1，0），C（x2，0），且x2﹣x1=4，直线AD∥x轴，在x轴上有一动点E（t，0）过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q．

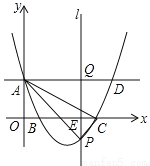
    （1）求抛物线的解析式；

    （2）当0＜t≤8时，求△APC面积的最大值；

    （3）当t＞2时，是否存在点P，使以A、P、Q为顶点的三角形与△AOB相似？若存在，求出此时t的值；若不存在，请说明理由．

    （1）；（2）12；（3）t=或t=或t=14． 【解析】试题分析：（1）首先利用根与系数的关系得出： ，结合条件求出的值，然后把点B，C的坐标代入解析式计算即可；（2）（2）分0＜t＜6时和6≤t≤8时两种情况进行讨论，据此即可求出三角形的最大值；（3）（3）分2＜t≤6时和t＞6时两种情况进行讨论，再根据三角形相似的条件，即可得解． 试题解析：【解析】 （1）由题意知x1、x2是...

    查看答案和解析>>

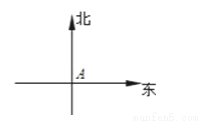
    科目：初中数学 来源：湖南省2017-2018学年七年级数学上期末复习检测数学试卷 题型：填空题

    一个人从A点出发向北偏东30°方向走到B点，再从B点出发向南偏东15°方向走到C点，那么∠ABC等于________ 度

    45 【解析】根据方位角的概念，画图正确表示出方位角，即可求解． 【解析】 由题意可知，∠1=30°，∠3=15°， ∵∠2=∠1=30° ∴∠ABC=∠2+∠3=30°+15°=45°． 故答案为：45°.

    查看答案和解析>>

    同步练习册答案