练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

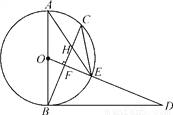
    如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BC于点F，交⊙O于点E，AE与BC交于点H，点D为OE的延长线上一点，且∠ODB＝∠AEC.

    求证：(1)BD是⊙O的切线；(2)CE2＝EH·EA.

    （1）证明见解析；（2）证明见解析. 【解析】试题分析：（1）由圆周角定理和已知条件证出∠ODB=∠ABC，再证出∠ABC+∠DBF=90°，即∠OBD=90°，即可得出BD是⊙O的切线；（2）连接AC，由垂径定理得出，即可得出∠CAE=∠ECB，再由公共角∠CEA=∠HEC，证明△CEH∽△AEC，得出对应边成比例，即可得出结论. 试题解析：(1)∵∠ODB＝∠AEC，∠AEC＝∠A...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级数学下2.2.1 用“同位角、第三直线”判定平行线 同步练习 题型：填空题

    如图,点B在DC上,BE平分∠ABD,∠ABE=∠C,试说明:BE∥AC.

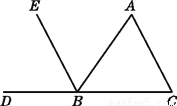
    解:因为BE平分∠ABD,

    所以∠ABE=∠DBE

    (_____________________). 

    因为∠ABE=∠C,

    所以∠DBE=∠C,

    所以BE∥AC(_____________________).

    角平分线的定义;同位角相等,两直线平行 【解析】根据角平分线的定义和平行线的判定填空，因为BE平分∠ABD, 所以∠ABE=∠DBE(角平分线的定义). 因为∠ABE=∠C, 所以∠DBE=∠C, 所以BE∥AC(同位角相等,两直线平行). 故答案为：角平分线的定义，同位角相等,两直线平行.

    查看答案和解析>>

    科目：初中数学 来源：江苏省张家港市2017-2018学年第一学期初三数学期末考试试卷 题型：解答题

    已知二次函数.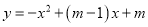

    (1)证明:不论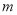取何值，该函数图像与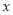轴总有公共点;

    (2)若该函数的图像与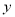轴交于点(0,3)，求出顶点坐标并画出该函数图像;

    (3)在(2)的条件下，观察图像，解答下列问题:

    ①不等式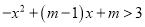的的解集是 ;

    ②若一元二次方程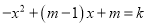有两个不相等的实数根，则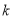的取值范围是 ;

    ③若一元二次方程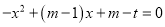在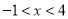的范围内有实数根，则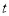的取

    值范围是 .

    （1）证明见解析；（2）顶点（1,4）；作图略(3)①0＜x＜2；②k＜4；③-5＜t≤4 【解析】试题分析：（1）令y=0得到关于x的方程，找出相应的a，b及c的值，表示出，整理配方后，根据完全平方式大于等于0，判断出大于等于0，可得出抛物线与x轴总有交点，得证； （2）由抛物线与y轴交于（0，3），将x=0，y=3代入抛物线解析式，求出m的值，进而确定出抛物线解析式，配方后找出顶点坐标...

    查看答案和解析>>

    科目：初中数学 来源：江苏省张家港市2017-2018学年第一学期初三数学期末考试试卷 题型：单选题

    如图，为⊙的直径，点在⊙上.若，则等于（）

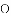
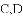
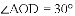
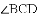
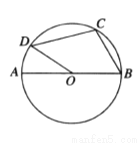
    A. 75° B. 95° C. 100° D. 105°

    D 【解析】试题解析：连接 故选D.

    查看答案和解析>>

    科目：初中数学 来源：江苏省张家港市2017-2018学年第一学期初三数学期末考试试卷 题型：单选题

    方程x（x﹣2）=0的解是（ ）

    A. x=0 B. x=2 C. x=0或x=﹣2 D. x=0或x=2

    D 【解析】试题分析：原方程已化为了方程左边为两个一次因式的乘积，方程的右边为0的形式；可令每一个一次因式为零，得到两个一元一次方程，从而求出原方程的解． 【解析】 由题意，得：x=0或x﹣2=0， 解得x=0或x=2；故选D．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：期中检测卷 题型：填空题

    正比例函数y1＝mx(m＞0)的图象与反比例函数y2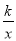＝ (k≠0)的图象交于点A(n，4)和点B，AM⊥y轴，垂足为M.若△AMB的面积为8，则满足y1＞y2的实数x的取值范围是____．

    －2＜x＜0或x＞2 【解析】正比例函数y1=mx（m>0）的图象与反比例函数y2=（k≠0）的图象交于点A（n，4）和点B， ∴B（-n，-4）． ∵△AMB的面积为8， ∴×8×n=8， 解得n=2， ∴A（2，4），B（-2，-4）． 由图形可知，当-22时，正比例函数y1=mx（m>0）的图象在反比例函数y2=（k≠0）图象的上方，即...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：期中检测卷 题型：单选题

    如图，在正方形ABCD中，点E为AB边的中点，点G，F分别为AD，BC边上的点，若AG＝1，BF＝2，∠GEF＝90°，则GF的长为( )

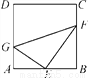
    A. 3 B. 4 C. 5 D. 6

    A 【解析】∵四边形ABCD是正方形， ∴∠A=∠B=90°， ∴∠AGE+∠AEG=90°，∠BFE+∠FEB=90°， ∵∠GEF=90°， ∴∠GEA+∠FEB=90°， ∴∠AGE=∠FEB，∠AEG=∠EFB． ∴△AEG∽△BFE， ∴ ， 又∵AE=BE， ∴AE2=AG•BF=2， ∴AE= ， ∴GF2=GE...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册数学 第二章 相交线与平行线 单元检测卷 题型：填空题

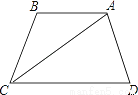
    如图，AB∥CD，∠D=80°，∠CAD：∠BAC=3：2，则∠CAD=________°．

    60 【解析】根据两直线平行，同旁内角互补求出∠BAD，再根据比例求解即可． 【解析】 ∵AB∥CD， ∴∠BAD=180°?∠D=180°?80°=100°， ∵∠CAD:∠BAC=3:2， ∴∠CAD=100°×=60°. 故答案为：60.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学北师大版上册 全册综合测试卷 题型：填空题

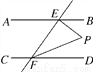
    如图，AB∥CD，EF与AB，CD分别相交于点E，F，EP⊥EF，与∠EFD的平分线FP相交于点P.若∠BEP＝46°，则∠EPF＝________°.

    68 【解析】由AB∥CD，根据两直线平行，同旁内角互补，即可得∠BEF+∠DFE=180°，又由EP⊥EF，∠EFD的平分线与EP相交于点P，∠BEP=46°，即可求得∠PFE的度数，然后根据三角形的内角和定理，即可求得∠EPF的度数． 【解析】 ∵AB∥CD， ∴∠BEF+∠DFE=180°， ∴EP⊥EF， ∴∠PEF=90°， ∵∠BEP=36°， ...

    查看答案和解析>>

    同步练习册答案