
��ͼ���ھ���ABCD�У�AD��2AB����E��F�ֱ���AD��BC���е㣬����AF��BE��CE��DF�ֱ��ڵ�M��N���㣬���ı���EMFN��(����)
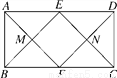
A. ������ B. ���� C. ���� D. ��ȷ��
A �����������ı���ABCDΪ���Σ� ��AD��BC��AD=BC�� �֡�E��F�ֱ�ΪAD��BC�е㣬 ��AE��BF,AE=BF,ED��CF��DE=CF�� ���ı���ABFEΪƽ���ı��Σ��ı���BFDEΪƽ���ı��Σ� ��BE��FD,��ME��FN�� ͬ����֤EN��MF�� ���ı���EMFNΪƽ���ı��Σ� ���ı���ABFEΪƽ���ı��Σ���ABCΪֱ�ǣ� ... ��Уͨ��֤��Ч��ҵϵ�д�
��Уͨ��֤��Ч��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ����ʦ�����꼶�²���ѧȫ���ۺϲ��Ծ� ���ͣ������
��ͼ����ABC�У�AB=AC����A=36�㣬AB���д���DE��AC��D����AB��E���������ۣ���1��BDƽ�֡�ABC����2��AD=BD=BC����3����BDC���ܳ�����AB+BC����4��D��AC�е㣮������ȷ�����������________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ2017-2018ѧ��Ⱦ��꼶���ϣ���ѧ��һ���¿��Ծ���11�·ݣ�(������) ���ͣ������
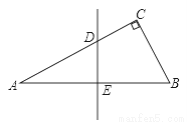
��֪Rt��ABC�У���ACB=90�㣬AC=6��BC=8����D��AB�е㣬��E��ֱ��AC��һ�㣬����C��D��EΪ��������������ABC���ƣ���AE�ij���Ϊ_____��
3�� ���������ߡ�ACB=90��,AC=6,BC=8, ��AB=62+82=10, �ߵ�D��AB�е�, ��CD=5, ��CD=AD, ���A=��ACD, ��C,D,EΪ��������������ABC���ƣ�Ӧ�֡�ABC�ס�CDE�͡�ABC�ס�CED���������������: ����ABC�ס�CDEʱ: , ��,��CE=3,�õ�:AE=3, ����ABC�ס�CE...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018����꼶�п���ѧר�⸴ϰͬ����ϰ�⣺ƽ���ı��� ���ͣ������
��֪AC������ABCD�ĶԽ��ߣ���BAC��60�㣬��E��ֱ��BC�ϵ�һ�����㣬����AE����AEΪ��������AEFG������ʹ��EAG��60�㣬����CG������E���߶�BC��ʱ����ͼ1����֤��AB��CG��CE.
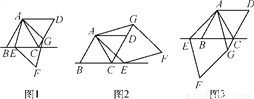
(1)����E���߶�BC���ӳ�����ʱ(��ͼ2)������AB��CG��CE֮��Ĺ�ϵ��֤����
(2)����E���߶�CB���ӳ�����ʱ(��ͼ3)��ֱ��д��AB��CG��CE֮��Ĺ�ϵ��
(1)AB��CG��CE(2)AB��CE��CG �������������������1���������ε����ʿɵ�AC=AD��AE=AG��Ȼ��֤����DAG=��CAE��������SAS֤����ACE�ա�ADG������ȫ�������ε����ʿɵ�CE=DG���ٸ����߶εĺͲ��ϵ�͵��������ɵô𰸣� ��2�������루1�����ƿ�֤����ACG�ա�ABE�������õ�BE=CG��Ȼ��ɵ�AB=CE��CG�� ���������(1)AB=CG-CE...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018����꼶�п���ѧר�⸴ϰͬ����ϰ�⣺ƽ���ı��� ���ͣ������
��ͼ�����ı���ABCD�У��Խ���AC��BD���ڵ�O��OA=OC��OB=OD������һ������ʹ�ı���ABCD�����Σ���ô�����ӵ������������� ����д��һ�����ɣ���
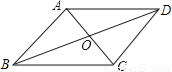
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018����꼶�п���ѧר�⸴ϰͬ����ϰ�⣺ƽ���ı��� ���ͣ���ѡ��
��ͼ����Rt��ABC�У���A��30�㣬BC��1����D��E�ֱ���ֱ�DZ�BC��AC���е㣬��DE�ij�Ϊ(����)
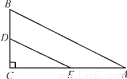
A. 1 B. 2 C. 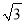 D. 1��
D. 1��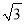
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ͼ���ڡ�ABC�У�AB=AC����ACΪֱ���ġ�O�ֱ�AB��BC�ڵ�M��N��ֱ��CP�ǡ�O�����ߣ��ҵ�P��AB���ӳ����ϣ�
��1������P=40�㣬���BCP�Ķ�����
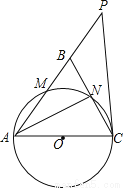
��2����BC=2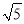 ��sin��BCP=
��sin��BCP=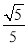 �����B��AC�ľ��룮
�����B��AC�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ͼ���뾶Ϊ13 cm��Բ����Ƭ������һ���Ϊ8 cm�Ĺ�����Ƭ��������AB�ij�Ϊ( )
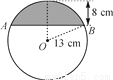
A. 10 cm B. 16 cm
C. 24 cm D. 26 cm
C �������������������O��OD��AB��C������O��D�������ù��ɶ������BC�ij����������ݴ��������ó�AB. �������� ��O��OD��AB��C������O��D�� ��CD=8��OD=13�� ��OC=OD-CD=5�� �֡�OB=13�� ��Rt��BCO�У�BC==12�� ��AB=2BC=24�� ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶�ϲ���ѧȫ���ۺϲ��Ծ� ���ͣ������
��a����С����Ȼ����b�����ĸ�������c�Ǿ���ֵ��С������������a��b��c�������ĺ�Ϊ________��
-1 ����������������������д����С����Ȼ�������ĸ���������ֵ��С������������a��b��c��ֵ������a+b+c��ֵ�� �������� ��Ϊ��С����Ȼ����0,���ĸ�������-1,����ֵ��С����������0�� ����a=0,b=-1,c=0, ����a+b+c=0-1+0=-1�� �ʴ���-1���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com