
在数轴上与表示2的点相距5个单位长度的点所表示的数是____________.
-3或7 【解析】试题解析:设数轴上与表示2的点相距5个单位长度的点代表的数是x, 则|x?2|=5, 解得x=7或x=?3. 故答案为:7或?3.科目:初中数学 来源:山西农业大学附属中学2017-2018学年八年级上学期第三次月考数学试卷 题型:单选题
用10米长的铝合金做成一个长方形的窗框(如图),设长方形窗框的横条长度为x米,则长方形窗框的面积为

A. 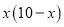 平方米 B.
平方米 B. 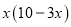 平方米
平方米
C. 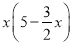 平方米 D.
平方米 D. 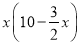 平方米
平方米
查看答案和解析>>
科目:初中数学 来源:江西省抚州市2017-2018年上学期九年级数学期末试卷 题型:解答题
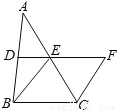
已知:如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.求证:四边形BCFE是菱形.
查看答案和解析>>
科目:初中数学 来源:广州市2018学年度七年级(上)数学期末测试卷 题型:解答题
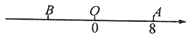
如图,数轴上点A表示的数为8,B是数轴上一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(l)点B表示的数为______,点P表示的数为_______(用含t的式子表示);
(2)动点H从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P,H同时出发,问点P运动多少秒时追上点H?
查看答案和解析>>
科目:初中数学 来源:广州市2018学年度七年级(上)数学期末测试卷 题型:填空题
观察下面一组式子:(1)1×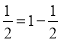 ; (2)
; (2)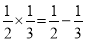 ;(3)
;(3)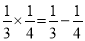 ;(4
;(4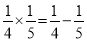 )…
)…
写出这组式子中的第(n)组式子是_____________________.
【解析】试题分析:如果把1看成,那么第一个分数的分母分别为1,2,3,4,…,则第n个数的分母为n,第二个分数的分母分别为2,3,4,…,则第n个数的分母为n+1,分子都是1,所以这组式子中的第n组式子是.故答案为.查看答案和解析>>
科目:初中数学 来源:广州市2018学年度七年级(上)数学期末测试卷 题型:单选题
如果am=an,那么下列等式不一定成立的是( )
A. am-3=an-3 B. 5+am=5+an C. m=n D. 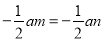
查看答案和解析>>
科目:初中数学 来源:广州市2018学年度七年级(上)数学期末测试卷 题型:单选题
-|-(-2)|的相反数( )
A. 2 B. 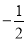 C. -2 D.
C. -2 D. 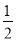
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省兰州市中考数学模拟试卷 题型:单选题
图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是( )
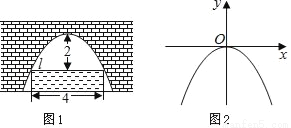
A. y=﹣2x2 B. y=2x2 C. y=﹣0.5x2 D. y=0.5x2
C 【解析】 由题意得,B(2,-2), 设二次函数解析式为:y=ax2, 将B(2,-2)代入解析式得:-2=4a,解得a=-0.5. 所以函数解析式为y= -0.5x2. 故选C.查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017年中考二模试卷数学试卷 题型:解答题
在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣2ax+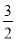 与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为C,直线AC交y轴于点D,D为AC的中点.
与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为C,直线AC交y轴于点D,D为AC的中点.
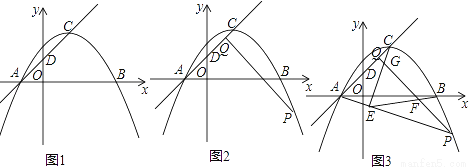
(1)如图1,求抛物线的顶点坐标;
(2)如图2,点P为抛物线对称轴右侧上的一动点,过点P作PQ⊥AC于点Q,设点P的横坐标为t,点Q的横坐标为m,求m与t的函数关系式;
(3)在(2)的条件下,如图3,连接AP,过点C作CE⊥AP于点E,连接BE、CE分别交PQ于F、G两点,当点F是PG中点时,求点P的坐标.
(1)C(1,2);(2)m=﹣t2+t+;(3)P(,﹣) 【解析】试题分析:(1)先由抛物线解析式确定出对称轴,再用中点坐标确定出点A的坐标,代入抛物线解析式确定出抛物线解析式,化为顶点式即可得出顶点坐标; (2)由(1)的条件,确定出直线AC解析式,由PQ⊥AC,确定出点P的坐标,消去y即可; (3)先判断出△ACE∽△APQ,再判断出∠ACB=90°,从而得到Rt△BCD...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com