
小颖家离学校1200米,其中有一段为上坡路,另一段为下坡路.她去学校共用了16分钟.假设小颖上坡路的平均速度是3千米/时,下坡路的平均速度是5千米/时.若设小颖上坡用了x分钟,下坡用了y分钟,根据题意可列方程组为( )
A. 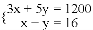 B.
B. 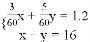 C.
C. 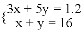 D.
D. 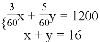
科目:初中数学 来源:四川省遂宁市2018届九年级上学期教学水平监测数学试卷 题型:单选题
方程x2+2x-5=0经过配方后,其结果正确的是
A. 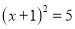 B.
B. 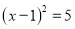
C. 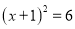 D.
D. 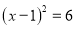
查看答案和解析>>
科目:初中数学 来源:2018春季学北师大版九年级数学下册期中测评试卷 题型:填空题
函数y=x2+2x+1,当y=0时,x=_____;当1<x<2时,y随x的增大而_____(填写“增大”或“减小”).
-1 增大 【解析】试题解析:当y=0时,x2+2x+1=0,即(x+1)2=0, 抛物线的对称轴为直线,且开口向上,故当1查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(人教版)期末检测题 题型:解答题
如图,若AB∥CD,∠1=∠2,∠3=∠4,AD与BC平行吗?为什么?
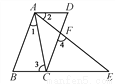
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(人教版)期末检测题 题型:填空题
规定用符号[m]表示一个实数m的整数部分,例如:[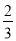 ]=0,[3.14]=3.按此规定[
]=0,[3.14]=3.按此规定[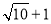 ]的值为_____.
]的值为_____.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(人教版)期末检测题 题型:单选题
代入法解方程组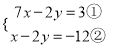 有以下步骤:(1)由①,得2y=7x-3③;(2)把③代入①,得7x-7x-3=3;(3)整理,得3=3;(4)∴x可取一切有理数,原方程组有无数组解.以上解法造成错误步骤是( )
有以下步骤:(1)由①,得2y=7x-3③;(2)把③代入①,得7x-7x-3=3;(3)整理,得3=3;(4)∴x可取一切有理数,原方程组有无数组解.以上解法造成错误步骤是( )
A. 第(1)步 B. 第(2)步 C. 第(3)步 D. 第(4)步
B 【解析】试题解析:错的是第步,应该将③代入②. 故选B.查看答案和解析>>
科目:初中数学 来源:湖北省武汉市洪山区2018届九年级(上)期中数学试卷 题型:解答题
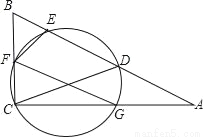
如图,D为Rt△ABC斜边AB上一点,以CD为直径的圆分别交△ABC三边于E、F、G三点,连接FE,FG.
(1)求证:∠EFG=∠B;
(2)若AC=2BC=4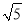 ,D为AE的中点,求FG的长.
,D为AE的中点,求FG的长.
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市洪山区2018届九年级(上)期中数学试卷 题型:单选题
如图,在平面直角坐标系xOy中,△ABC顶点的横、纵坐标都是整数.若将△ABC以某点为旋转中心,顺时针旋转90°得到△DEF,则旋转中心的坐标是( )
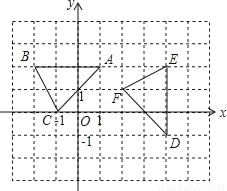
A. (0,0) B. (1,0) C. (1,﹣1) D. (2.5,0.5)
C 【解析】试题解析:∵将△ABC以某点为旋转中心,顺时针旋转90°得到△DEF, ∴点A的对应点为点D,点B的对应点为点E, 作线段AD和BE的垂直平分线,它们的交点为P(1,﹣1), ∴旋转中心的坐标为(1,﹣1). 故选C.查看答案和解析>>
科目:初中数学 来源:四川省西昌市2017-2018学年九年级数学(上)期末模拟试卷 题型:解答题
在体育课上,老师向排好队列的学生讲解行进间传球的要领时,叫甲、乙、丙、丁四位是年级球队队员的同学出列,配合老师进行传球示范.
(1)首先球在老师手里时,直接传给甲同学的概率是多少?
(2)当老师传给甲后,老师叫四位同学相互传球,其他人观看体会,当甲第一个传出,求甲传给下一个同学后,这个同学又再传回给甲的概率.
(1)先直接传给甲同学的概率是;(2)再传回甲的概率为. 【解析】试题分析:(1)直接根据概率公式计算即可; (2)先画树状图,再根据公式计算即可. 试题解析:(1)当球在老师手里时,先直接传给甲同学的概率是; (2)当甲传出球后,经两次传球的情况可用如下树状图表示: ∴再传回甲的概率为=.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com