
在Rt△ABC中,∠C=90°,BC=l,AC=2,那么cosB的值是( )
A. 2 B. 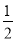 C.
C. 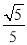 D.
D. 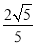
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:人教版2017-2018学年九年级下册数学全册综合测试卷 题型:单选题
如图,点N是反比例函数y=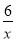 (x>0)图象上的一个动点,过点N作MN∥x轴,交直线y=﹣2x+4于点M,则△OMN面积的最小值是( )
(x>0)图象上的一个动点,过点N作MN∥x轴,交直线y=﹣2x+4于点M,则△OMN面积的最小值是( )
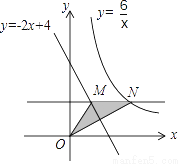
A. 1 B. 2 C. 3 D. 4
B 【解析】设点N的坐标为(,m),则点M的坐标为(4?2m,m)(m>0), ∴MN=?(4?2m)=2m+?4, ∴S△OMN=MN?m=m2?2m+3=(m?1)2+2, ∴当m=1时,△OMN面积最小,最小值为2. 故选:B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷1 题型:单选题
如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB,BD于M,N两点.若AM=2,则线段ON的长为( )
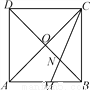
A. 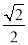 B.
B. 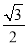 C. 1 D.
C. 1 D. 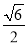
查看答案和解析>>
科目:初中数学 来源:江苏省张家港市2017-2018学年第一学期初三数学期末考试试卷 题型:填空题
一圆锥的母线长为6cm,它的侧面展开图的圆心角为120°,则这个圆锥的底面半径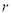 为
为
cm.
2 【解析】圆锥的侧面积为扇形,扇形的面积公式为:,代入求解即可. 圆锥的侧面积==12πcm2.查看答案和解析>>
科目:初中数学 来源:江苏省张家港市2017-2018学年第一学期初三数学期末考试试卷 题型:单选题
已知:关于x的一元二次方程x2﹣(R+r)x+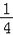 d2=0有两个相等的实数根,其中R、r分别是⊙O1、⊙O2的半径,d为两圆的圆心距,则⊙O1与⊙O2的位置关系是( )
d2=0有两个相等的实数根,其中R、r分别是⊙O1、⊙O2的半径,d为两圆的圆心距,则⊙O1与⊙O2的位置关系是( )
A. 外离 B. 外切 C. 相交 D. 内含
B 【解析】试题解析:由题中有两个相等的实数根可得, 即R+r=d,由圆与圆的位置关系判定法则可知,两圆的位置关系是外切. 故选B.查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:期中检测卷 题型:解答题
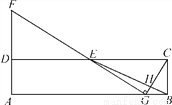
如图,在矩形ABCD中,E为CD的中点,H为BE上的一点, 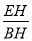 =3,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
=3,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
(1)求证: 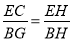 ;
;
(2)若∠CGF=90°,求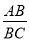 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:期中检测卷 题型:填空题
如图,反比例函数y=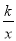 (x>0)的图象交Rt△OAB的斜边OA于点D,交直角边AB于点C,点B在x轴上.若△OAC的面积为5,AD∶OD=1∶2,则k的值为______.
(x>0)的图象交Rt△OAB的斜边OA于点D,交直角边AB于点C,点B在x轴上.若△OAC的面积为5,AD∶OD=1∶2,则k的值为______.
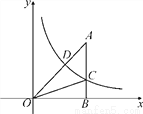
查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册数学 第二章 相交线与平行线 单元检测卷 题型:解答题
如图,已知直线AB∥DF,∠D+∠B=180°,
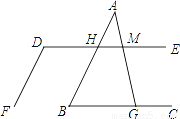
(1)求证:DE∥BC;
(2)如果∠AMD=75°,求∠AGC的度数.
(1)证明见解析;(2)105°. 【解析】(1)根据平行线的性质得出∠D+∠BHD=180°,等量代换得出∠B=∠DHB,根据平行线的判定得出即可; (2)根据平行线的性质求出∠AGB=∠AMD=75°,再根据邻补角的定义即可求出∠AGC的度数. (1)证明:∵AB∥DF, ∴∠D+∠BHD=180°, ∵∠D+∠B=180°, ∴∠B=∠DHB, ∴D...查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学北师大版上册 全册综合测试卷 题型:解答题
如图,已知直线CB∥OA,∠C=∠OAB=100°,点E、F在线段BC上,满足∠FOB=∠AOB=α,OE平分∠COF.

(1)用含有α的代数式表示∠COE的度数;
(2)若沿水平方向向右平行移动AB,则∠OBC∶∠OFC的值是否发生变化?若变化,找出变化规律;若不变,求其比值.
(1)∠COE=40°-α;(2)∠OBC∶∠OFC=1∶2. 【解析】(1)先根据平行线的性质得出∠AOC的度数与∠FBO=∠AOB,再由∠FOB=∠AOB,得出∠FBO=∠FOB即OB平分∠AOF,根据OE平分∠COF,可知∠EOB=∠EOF+∠FOB,故可得出结论; (2)根据平行线的性质可得出∠OBC=∠BOA,∠OFC=∠FOA,从而得出答案. 【解析】 (1)∵CB...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com