
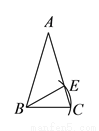
如图,已知等腰三角形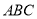 ,
, 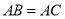 ,若以点
,若以点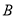 为圆心,
为圆心, 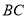 长为半径画弧,交腰
长为半径画弧,交腰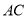 于点
于点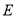 ,则下列结论一定正确的是( )
,则下列结论一定正确的是( )
A. 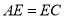 B.
B. 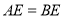 C.
C. 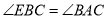 D.
D. 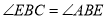
科目:初中数学 来源:2017-2018学年八年级数学北师大版上册 第4章 一次函数 单元测试卷 题型:填空题
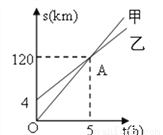
如图,射线OA、BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s、t分别表示行驶距离和时间,则这两人骑自行车的速度相差_______km/h.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版16.2二次根式定义的乘除同步练习 题型:填空题
已知三角形的一边长为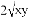 ,这边上的高为
,这边上的高为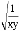 ,则这个三角形的面积是______.
,则这个三角形的面积是______.
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2017-2018学年八年级上学期期中数学 题型:解答题
已知,如图,四边形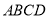 ,
, 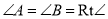 .
.
( )用直尺和圆规,在线段
)用直尺和圆规,在线段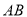 上找一点
上找一点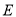 ,使得
,使得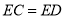 ,连接
,连接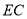 ,
, 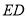 (不写作法,保留作图痕迹).
(不写作法,保留作图痕迹).
(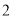 )在(
)在(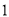 )的图形中,若
)的图形中,若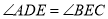 ,且
,且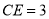 ,
, 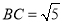 ,求
,求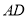 的长.
的长.

查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2017-2018学年八年级上学期期中数学 题型:单选题
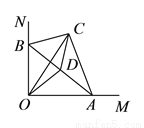
如图,在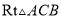 中,
中, 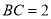 ,
, 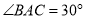 ,斜边
,斜边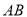 的两个端点分别在相互垂直的射线
的两个端点分别在相互垂直的射线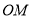 、
、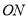 上滑动,下列结论:①若
上滑动,下列结论:①若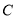 、
、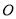 两点关于
两点关于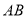 对称,则
对称,则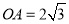 ;②
;②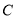 、
、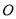 两点距离的最大值为
两点距离的最大值为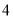 ;③若
;③若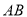 平分
平分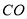 ,则
,则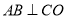 ;④ 四边形
;④ 四边形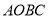 的面积为
的面积为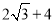 .其中正确结论的个数是( )
.其中正确结论的个数是( )
A. 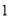 B.
B. 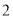 C.
C. 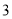 D.
D. 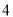
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第三章圆单元检测卷 题型:解答题
.如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交劣弧CB于D,连接AC.
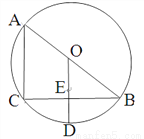
(1)请写出两个不同的正确结论;
(2)若CB=8,ED=2,求⊙O的半径.
(1)见解析;(2)5. 【解析】试题分析:(1)可以从线段的关系、角的关系、三角形的关系等等方面说明;(2)设的半径等于R,利用垂经定理和勾股定理可求出圆的半径. 试题解析:(1)不同类型的正确结论有:①BE=CE;②BD=CD;③∠BED=90°;④∠BOD=∠A;⑤AC//OD;⑥AC⊥BC;⑦;⑧;⑨△BOD是等腰三角形;⑩;等等。 (2)∵ OD⊥CB ∴BE=CE= ...查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第三章圆单元检测卷 题型:填空题
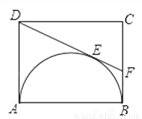
矩形ABCD中,AB=4,AD=3,以AB为直径在矩形内作半圆.DE切⊙O于点E(如图),则tan∠CDF的值为________ .
查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试卷 题型:解答题
某校九年级进行了模拟考试后,张老师对九(2)班全体同学“满分值为6分得一道解答题的得分”情况进行了统计,绘制成下表(学生得分均为整数分):

由于在填表时不慎把墨水滴在表格上,致使表中数据不完整,但已知全班同学此题的平均得分为4分,结合上表回答下列问题:
(1)九(2)班学生共有多少人?
(2)若本年级学生共有540人,请你用此样本估计整个年级有多少同学此题得满分?
(1)45(人);(2)估计该校九年级有132人此题得满分. 【解析】试题分析:(1)设该班得6分的学生为x人,然后根据“全班同学此题的平均得分为4分”列出方程求解即可; (2)利用本班中得满分的学生占全班学生的比例即可求出整个年级有多少同学此题得满分. 试题解析::(1)设该班得6分的学生为x人, 则根据题意得:1×1+2×5+3×7+4×8+5×10+6x=(3+1+5...查看答案和解析>>
科目:初中数学 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
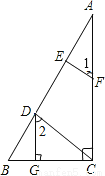
如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com