
(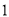 )如图
)如图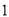 ,
, 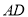 是
是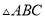 形内的高,
形内的高, 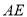 是
是 的外接圆⊙
的外接圆⊙ 的直径.
的直径.
①求证: 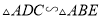 .
.
②若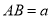 ,
, 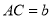 ,
, 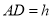 ,⊙
,⊙ 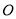 的直径
的直径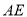 长.
长.
③如图,在边长为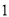 的小正方形组成的网格之中有一个格点三角形
的小正方形组成的网格之中有一个格点三角形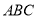 ,请你从上面两小题中获得经验,直接写出此格点三角形的外接圆面积.
,请你从上面两小题中获得经验,直接写出此格点三角形的外接圆面积.
( )如图
)如图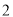 ,
, 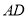 是
是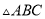 形外的高,若
形外的高,若 ,
, 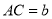 ,
, 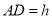 ,(
,(  )题中②的结论是否还成立?成立与否都要说明理由.
)题中②的结论是否还成立?成立与否都要说明理由.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源:2017-2018学年七年级数学北师大版上册:第2章 有理数及其运算 单元测试卷 题型:单选题
已知点A是数轴上的一点,且点A到原点的距离为2,把点A沿数轴向右移动5个单位得到点B,则点B表示的有理数是( )
A. 7 B. -3 C. 7或3 D. -7或-3
C 【解析】离原点2的点是2+5=5,-2+5=3,所以选C.查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 第一章 整式的乘除 1.1 同底数幂的乘法 同步测试 含答案 题型:填空题
已知am=3,an=2,则am+n的值为__.
6 【解析】试题解析:∵am=3,an=2, ∴am+n= am×an=3×2=6. 故答案为:6.查看答案和解析>>
科目:初中数学 来源:2018届中考数学一轮复习单元检测:第7讲 一元二次方程(组)及应用 题型:解答题
关于x的一元二次方程ax2+bx+c=0(a≠0)的两根为x1=1,x2=-1,那么下列结论一定成立的是( )
A. b2-4ac>0 B. b2-4ac=0
C. b2-4ac<0 D. b2-4ac≤0
A 【解析】∵x1=1,x2=-1, ∴x1≠x2, ∴方程有两个不相等的实数根; ∴b2-4ac>0. 故选A.查看答案和解析>>
科目:初中数学 来源:2018届中考数学一轮复习单元检测:第7讲 一元二次方程(组)及应用 题型:单选题
广州亚运会的某纪念品原价188元,连续两次降价a%后售价为118元,下列所列方程中正确的是( )
A. 188(1+a%)2=118 B. 188(1-a%)2=118
C. 188(1-2a%)=118 D. 188(1-a2%)=118
B 【解析】当商品第一次降价a%时,其售价为168(1?a%); 当商品第二次降价a%后,其售价为168(1?a%) ·(1?a%) =168(1?a%)2. ∴168(1?a%)2=128. 故选B.查看答案和解析>>
科目:初中数学 来源:浙江杭州上城区建兰中学2018届九年级上学期期中数试卷 题型:解答题
有一箱子装有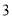 张分别标示
张分别标示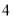 、
、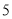 、
、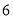 的号码牌,已知小武以每次取一张且取后不放回的方式,先后取出
的号码牌,已知小武以每次取一张且取后不放回的方式,先后取出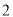 张牌,组成一个二位数,取出第
张牌,组成一个二位数,取出第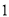 张牌的号码为十位数,第
张牌的号码为十位数,第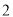 张牌的号码为个位数,若先后取出
张牌的号码为个位数,若先后取出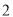 张牌组成二位数的每一种结果发生的机会都相同,用列表或树状表示组成二位数的可能情况,并求组成的二位数为
张牌组成二位数的每一种结果发生的机会都相同,用列表或树状表示组成二位数的可能情况,并求组成的二位数为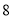 的倍数的概率.
的倍数的概率.
查看答案和解析>>
科目:初中数学 来源:浙江杭州上城区建兰中学2018届九年级上学期期中数试卷 题型:单选题
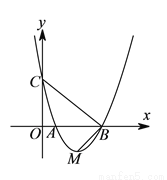
如图,抛物线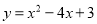 与
与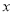 轴交于
轴交于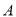 ,
, 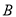 两点,与
两点,与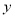 轴交于点
轴交于点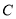 ,顶点为
,顶点为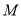 ,连结
,连结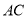 ,
, 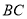 .在
.在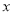 轴上是否存在点
轴上是否存在点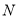 ,使以
,使以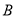 ,
, 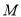 ,
, 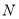 为顶点的三角形与
为顶点的三角形与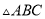 相似,则满足条件的所有
相似,则满足条件的所有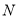 点的坐标为( )
点的坐标为( )
A. 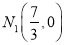 ,
, 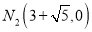 B.
B. 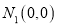 ,
, 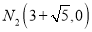
C. 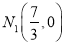 ,
, 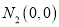 ,
, 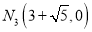 D.
D. 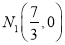 ,
, 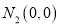
查看答案和解析>>
科目:初中数学 来源:广东省汕头市龙湖区2018届九年级上学期期末质量检测数学试卷 题型:解答题
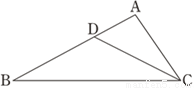
如图,△ABC中,点D在边AB上,满足∠ACD=∠ABC,若AC=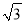 ,AD=1,求DB的长.
,AD=1,求DB的长.
查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学全册综合测试一 题型:填空题
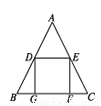
如图,△ABC中,AB=AC,点D,E分别是边AB,AC的中点,点G,F在BC边上,四边形DEFG是正方形.若DE=2 cm,则AC的长为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com