练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    半径为3的圆中，扇形AOB的圆心角为150°，请在图中圆内画出这个扇形，并求出它的面积．(结果保留π)

    π. 【解析】试题分析：用150°占360°的比例乘以圆的面积即可． 试题解析：【解析】 如图． 扇形AOB的面积为＝.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：重庆市江北区联盟校2018届九年级（上）期中数学试卷 题型：单选题

    （2016重庆，第9题，4分）观察下列一组图形，其中图形①中共有2颗星，图形②中共有6颗星，图形③中共有11颗星，图形④中共有17颗星，…，按此规律，图形⑧中星星的颗数是（　　）

    A. 43 B. 45 C. 51 D. 53

    C 【解析】试题解析：设图形n中星星的颗数是an（n为正整数）， ∵a1=2=1+1，a2=6=（1+2）+3，a3=11=（1+2+3）+5，a4=17=（1+2+3+4）+7， ∴an=1+2+…+n+（2n-1）=+（2n-1）=n2+n-1， ∴a8=×82+×8-1=51． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：北京师范大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型：单选题

    在数8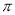，- ，0，-|-2|，-0.5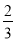，-，-1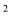中，负数的个数有

    A. 3 B. 4 C. 5 D. 6

    C 【解析】8是正数；0既不是正数，也不是负数； -π，-|-2|，-0.5，- ，-12是负数，共5个. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册 第四章 基本平面图形练习题 题型：解答题

    如图，线段AB＝10 cm，延长AB到点C，使BC＝6 cm，点M、N分别为AC、BC的中点，求线段BM、MN的长．

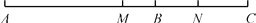
    2cm，5cm． 【解析】试题分析：AB和BC长度已知，则可求出AC长度，点M是AC中点，MC等于AC长度的一半，点N是BC中点，NC长度是BC的一半，MN的长度等于MC﹣NC，从而可得出MN的长度．线段BM的长度AB的长度减去AM的长度，AB的长度已知，AM的长度为AC的一半也可求出． 试题解析：【解析】 ∵AB=10，BC=6 ∴AC=16 又∵M为AC的中点∴MC=...

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册 第四章 基本平面图形练习题 题型：解答题

    请利用圆规，找出图中的扇形(不要添加其他线)，看一看每个图中各有多少个扇形？

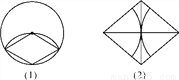
    (1)有3个扇形；(2)有6个扇形． 【解析】试题分析：根据扇形的定义：由两条半径，和连接两条半径的一段弧组成的图形叫做扇形，结合图形即可得出答案． 试题解析：【解析】 （1）在图中不是每一个弧都对应一个扇形，由此可得图形中有3个扇形． （2）根据扇形的定义可得图中有6个扇形．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册 第四章 基本平面图形练习题 题型：填空题

    一个正六边形的周长是18 cm，则这个正六边形的边长是________cm.

    3 【解析】【解析】 正六边形的边长=18÷6=3．故答案为：3．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册 第四章 基本平面图形练习题 题型：单选题

    下列图形中，不是多边形的是( )

    A.

    B.

    C.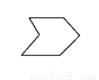

    D.

    D 【解析】解：A、B、C中的图形都是由线段首尾顺次连结构成的图形，是多边形，D中图形由线段和曲线构成，不是多边形．故选D．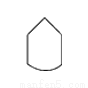

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册 第四章 基本平面图形练习题 题型：单选题

    为比较两条线段AB与CD的大小，小明将点A与点C重合使两条线段在一条直线上，点B在CD的延长线上，则( )

    A. AB＜CD B. AB＞CD C. AB＝CD D. 以上都有可能

    B 【解析】【解析】 由点A与点C重合使两条线段在一条直线上，点B在CD的延长线上，得AB＞CD．故选B．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册 第四章 基本平面图形练习题 题型：解答题

    如图，数轴上A，B两点对应的有理数分别为10和15，点P从点A出发，以每秒1个单位长度的速度沿数轴正方向运动，点Q同时从原点O出发，以每秒2个单位长度的速度沿数轴正方向运动，设运动时间为t秒．

    (1)当0＜t＜5时，用含t的式子填空：

    BP＝_______，AQ＝_______；

    (2)当t＝2时，求PQ的值；

    (3)当PQ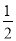＝AB时，求t的值．

    (1)5－t,10－2t；（2）8；(3)t=12.5或7.5. 【解析】试题分析：（1）先求出当0＜t＜5时，P点对应的有理数为10+t＜15，Q点对应的有理数为2t＜10，再根据两点间的距离公式即可求出BP，AQ的长； （2）先求出当t=2时，P点对应的有理数为10+2=12，Q点对应的有理数为2×2=4，再根据两点间的距离公式即可求出PQ的长； （3）由于t秒时，P...

    查看答案和解析>>

    同步练习册答案