
��2016���죬��9�⣬4�֣��۲�����һ��ͼ�Σ�����ͼ���й���2���ǣ�ͼ���й���6���ǣ�ͼ���й���11���ǣ�ͼ���й���17���ǣ��������˹��ɣ�ͼ�������ǵĿ����ǣ�������

A. 43 B. 45 C. 51 D. 53
C �������������������ͼ��n�����ǵĿ�����an��nΪ���������� ��a1=2=1+1��a2=6=��1+2��+3��a3=11=��1+2+3��+5��a4=17=��1+2+3+4��+7�� ��an=1+2+��+n+��2n-1��=+��2n-1��=n2+n-1�� ��a8=��82+��8-1=51�� ��ѡC��
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��ɽ��ʡ2018����꼶����ĩģ����ѧ�Ծ� ���ͣ���ѡ��
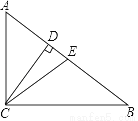
��ͼ����Rt��ABC�У���ACB=90�㣬CD��CE�ֱ���б���ϵĸߺ����ߣ���AC=CE=6����CD�ij�Ϊ�� ��
A. 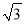 B. 3
B. 3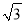 C. 6 D. 6
C. 6 D. 6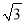
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����з���2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
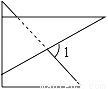
��һ�����dz߰���ͼ��ʾ�ķ�ʽ���ã�ʹ��30��ǵ����dzߵĶ�ֱ�DZߺͺ�45��ǵ����dzߵ�һ��ֱ�DZ��غϣ����1�Ķ������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������н���������У2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
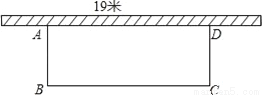
��ͼ��ʾ��ѧУ���ڽ�ѧ¥����һ�����������г����һ�����ý�ѧ¥�ĺ�ǽ�������õ�ǽ��Ϊ19m����������������ѧУ�����ܳ�38m������Χ�ɣ�
��1����Χ�ɵ����Ϊ180m2����������г�����ij��Ϳ���
��2����Χ�ɵ����Ϊ200m2���г�����������ܣ����������Ʒ�����������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������н���������У2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
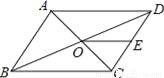
��ͼ��ƽ���ı���ABCD���ܳ�Ϊ36���Խ���AC��BD�ཻ�ڵ�O����E��CD���е㣬BD=12�����DOE���ܳ���_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������н���������У2018����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
��һԪ���η���x2+2x+a=0����ʵ���⣬��a��ȡֵ��Χ�ǣ�������
A. a��1 B. a��4 C. a��1 D. a��1
C �������������������һԪ���η���x2+2x+a=0����ʵ���⣬������б�ʽ����0���ݴ˿����г�����a�IJ���ʽ��ͨ���ⲻ��ʽ�������a��ֵ�� �������� ��Ϊ����x��һԪ���η�����ʵ���� ���ԡ�=b2��4ac=4��4a��0�� ��֮��a��1�� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʦ����ѧ������ѧ2017-2018ѧ�����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��֪��������a��b���ɰ�����c=ab+a+b����Ϊһ������c����a��b��c��������ȡ�����ϴ��������������������õ�һ��������������ȥ����ÿ����һ�εõ�һ��������Ϊһ�β�����
��1����a=1��b=3���������������3�Σ��������õ�����__________��
��2����p>q>0������3�β������������õ���Ϊ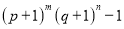 ��m��nΪ������������m��n��ֵ�ֱ�Ϊ__________.
��m��nΪ������������m��n��ֵ�ֱ�Ϊ__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʦ����ѧ������ѧ2017-2018ѧ�����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��֪������a�������ϵ�λ����ͼ����a+|a-1|=__________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�ϲ� ������ ����ƽ��ͼ����ϰ�� ���ͣ������
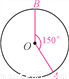
�뾶Ϊ3��Բ�У�����AOB��Բ�Ľ�Ϊ150�㣬����ͼ��Բ�ڻ���������Σ���������������(���������)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com