练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

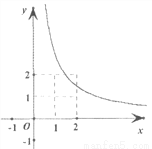
    反比例函数y=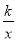在第一象限的图象如图，请写出一个满足条件的k值，k=__________.

    答案不唯一，如：k=3. 【解析】∵反比例函数y=的图象在第一象限， ∴k>0， 根据点（2，1）和点（2，2）不在这个反比例函数图象上，可知2
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：重庆市江津区2017-2018学年八年级上学期第二次六校联考数学试卷 题型：单选题

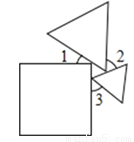
    一个正方形和两个等边三角形的位置如图所示，若∠3=50°，则∠1+∠2=（　　）

    A. 90° B. 100° C. 130° D. 180°

    B 【解析】试题解析：如图， ∠BAC=180°-90°-∠1=90°-∠1，. ∠ABC=180°-60°-∠3=120°-∠3，. ∠ACB=180°-60°-∠2=120°-∠2，. 在△ABC中，∠BAC+∠ABC+∠ACB=180°，. ∴90°-∠1+120°-∠3+120°-∠2=180°，. ∴∠1+∠2=150°-∠3，. ∵∠3=...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷（C卷） 题型：填空题

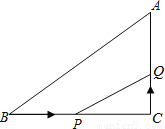
    如图，在△ABC中，∠C=90°，BC=16cm，AC=12cm，点P从点B出发，沿BC以2 cm /s的速度向点C移动，点Q从点C出发，以1cm/s的速度向点A移动，若点P、Q分别从点B、C同时出发，设运动时间为ts，当t＝________时，△CPQ与△CBA相似．

    或4.8 【解析】试题分析：当CP和CB是对应边时，△CPQ∽△CBA，所以，即，解得t=4.8； 当CP和CA是对应边时，△CPQ∽△CAB，所以，即，解得t=． 综上所述，当t=4.8秒或秒时，△CPQ与△CBA相似．

    查看答案和解析>>

    科目：初中数学 来源：北京四中2018届上学期初中九年级期中考试数学试卷 题型：解答题

    问题探究：

    新定义：

    将一个平面图形分为面积相等的两部分的直线叫做该平面图形的“等积线”，其“等积线”被该平面图形截得的线段叫做该平面图形的“等积线段”（例如圆的直径就是圆的“等积线段”）

    解决问题：

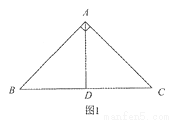
    已知在Rt△ABC中，∠BAC=90°，AB=AC=2.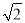

    （1）如图1，若AD⊥BC，垂足为D，则AD是△ABC的一条等积线段，直接写出AD的长；

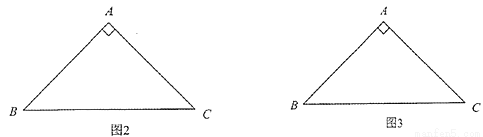
    （2）在图2和图3中，分别画出一条等积线段，并直接写出它们的长度. （要求：图1、图2和图3中的等积线段的长度各不相等）

    （1）AD=2；（2）符合题意的图形见解析，BE=，GH=2 【解析】试题分析：（1）根据等腰直角三角形的性质，底边上的高线即可求得； （2）作中线BE，中线BE即为一条等积线，利用勾股定理即可求得长度； 作GH//BC，GH将Rt△ABC的面积分为相等的两份，则GH即为一条等积线，根据相似三角形的性质即可求得长度. 试题解析：（1）在Rt△ADC中， ∵AC=2，∠...

    查看答案和解析>>

    科目：初中数学 来源：北京四中2018届上学期初中九年级期中考试数学试卷 题型：解答题

    若二次函数y=x2+bx+c的图象经过点（0，1）和（1，-2）两点，求此二次函数的表达式.

    二次函数的表达式为y=x2-4x+1. 【解析】试题分析：把点（0，1）和（1，-2）分别代入二次函数的解析式，利用待定系数法进行求解即可得. 试题解析：∵二次函数y=x2+bx+c的图象经过（0，1）和（1，-2）两点， ∴ 解得 ∴二次函数的表达式为y=x2-4x+1.

    查看答案和解析>>

    科目：初中数学 来源：北京四中2018届上学期初中九年级期中考试数学试卷 题型：单选题

    如图，D，E为△ABC的边AB，AC上的点，DE∥BC，若AD：DB=1：3，AE=2，则AC的长是（ ）.

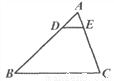
    A. 10 B. 8 C. 6 D. 4

    B 【解析】∵DE//BC， ∴AE：EC=AD：DB， ∵AD：DB=1：3， ∴AE：EC=1：3， ∵AE=2，∴EC=6， ∴AC=AE+EC=8， 故选B.

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省张掖市中考数学三模试卷 题型：解答题

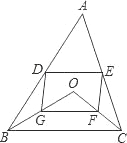
    D、E分别是不等边三角形ABC（即AB≠BC≠AC）的边AB、AC的中点．O是△ABC所在平面上的动点，连接OB、OC，点G、F分别是OB、OC的中点，顺次连接点D、G、F、E．

    （1）如图，当点O在△ABC的内部时，求证：四边形DGFE是平行四边形；

    （2）若四边形DGFE是菱形，则OA与BC应满足怎样的数量关系？（直接写出答案，不需要说明理由．）

    （1）证明见解析；（2）当OA=BC时，平行四边形DEFG是菱形． 【解析】试题分析：（1）根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC且DE=BC，GF∥BC且GF=BC，从而得到DE∥GF，DE=GF，再利用一组对边平行且相等的四边形是平行四边形证明即可； （2）根据邻边相等的平行四边形是菱形解答． 试题解析：（1）∵D、E分别是AB、AC边的中点， ...

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省张掖市中考数学三模试卷 题型：单选题

    抛物线y=ax2+bx+c（a≠0）的图象如图所示，则下列说法正确的是（　　）

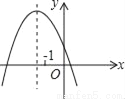
    A. b2﹣4ac＜0 B. abc＜0 C. 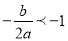D. a﹣b+c＜0

    C 【解析】抛物线开口向下，所以，对称轴在-1的左侧，所以，抛物线与横轴有两个交点，说明b2﹣4ac大于0，C正确，故选C

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省随州市中考数学模拟试卷 题型：填空题

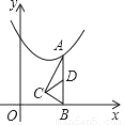
    如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+3上运动,过点A作AB⊥x轴于点B,以AB为斜边作Rt△ABC,则AB边上的中线CD的最小值为______．

    1. 【解析】试题分析：根据题意可知，当A点在抛物线的顶点（1，2）时，AB的长最短，最短为2，这时根据直角三角形斜边上的中线等于斜边的一半，可直接求解为CD=1. 故答案为：1.

    查看答案和解析>>

    同步练习册答案