练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    解方程：x2＋4x＝1．

    ， ． 【解析】分析：方程两边加上4得到(x+2)²=5，然后利用直接开平方法解方程. 本题解析： 解： ∴ ∴
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：黑龙江省大庆市2016---2017学年度上期初三数学期末试卷 题型：单选题

    关于x的分式方程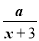=1，下列说法正确的是（　　）

    A. 方程的解是x=a-3 B. 当a＞3时，方程的解是正数

    C. 当a＜3时，方程的解为负数 D. 以上答案都正确

    B 【解析】方程两边都乘以x+3，去分母得：a=x+3， 解得：x=a?3， ∴当x+3≠0，把x=a?3代入得：a?3+3≠0，即a≠0，方程有解，故选项A错误； 当x>0，即a?3>0，解得：a>3，则当a>3时，方程的解为正数，故选项B正确； 当x<0，即a?3<0，解得：a<3，则a<3且a≠0时，方程的解为负数，故选项C错误； 显然选项D错误。 ...

    查看答案和解析>>

    科目：初中数学 来源：南京市玄武区2016~2017学年度第一学期期九年级试卷 题型：解答题

    一只不透明的袋子中装有1个蓝球和2个红球，这些球除颜色外都相同．

    （1）搅匀后从中任意摸出1个球，求摸到蓝球的概率；

    （2）搅匀后从中任意摸出1个球，记录颜色后放回、搅匀，再从中任意摸出1个球．

    求至少有1次摸到红球的概率．

    （1）；（2）． 【解析】分析：(1)列举出所有的可能结果,找到恰是蓝球的结果,根据概率公式计算即可, (2)列举出所有可能出现的结果,找到至少有一次是红球的结果,根据概率公式计算即可. 本题解析： (1)搅匀后从中任意摸出1个球,所有可能出现的结果有:红、红、蓝、共有3种,它们出现的可能性相同.所有的结果中,满足“恰好是蓝球”(记为事件A)的结果只有1种,所以;. ...

    查看答案和解析>>

    科目：初中数学 来源：南京市玄武区2016~2017学年度第一学期期九年级试卷 题型：单选题

    在比例尺为1∶500000的工程图上，南京地铁四号线全长约6.76 cm，它的实际长度约为（　　）

    A. 3.38 km B. 338 km C. 33.8 km D. 0.338 km

    C 【解析】解:设地铁线的实际长度约为xcm. 根据比例尺的定义:比例尺=图上距离:实地距离,可得 解之得 x=33800000 ∵ 33800000cm=33.8km ∴ 它的实际长度为33.8km 故选C.

    查看答案和解析>>

    科目：初中数学 来源：南京市溧水区2016~2017学年度第一学期期末九年级试卷 题型：解答题

    已知函数y＝x2＋2kx＋k2+1．

    （1）求证：不论k取何值，函数y＞0；

    （2）若函数图象与y轴的交点坐标为（0，5），求函数图象的顶点坐标．

    （1）答案见解析；（2）顶点坐标为（2，1）或（－2，1）． 【解析】分析:(1)由根的判别式小于0，可知抛物线与x轴无交点，再由图象开口向上可得出结论；（2）由二次函数图像与y轴的交点可得出k2+1=5，得出k 的值，代入原函数即可. 本题解析： 【解析】 （1）解法一：∵a=1，b=2k，c=k2+1 ∴b2－4ac=（2k）2－4×1×（k2+1）=－4＜0 ...

    查看答案和解析>>

    科目：初中数学 来源：南京市溧水区2016~2017学年度第一学期期末九年级试卷 题型：填空题

    如图，AB∥CD，S△ABE：S△CDE=1：4，则=___________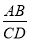

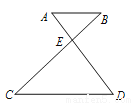
    【解析】∵AB∥CD，∴S△ABE∽S△CDE，∴ , ∵S△ABE：S△CDE=1：4, ∴= ，故答案为.

    查看答案和解析>>

    科目：初中数学 来源：南京市溧水区2016~2017学年度第一学期期末九年级试卷 题型：单选题

    某同学在用描点法画二次函数y=ax2+bx+c的图象时，列出了下面的表格：

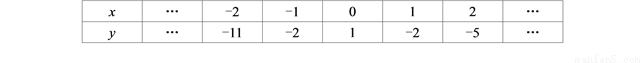
    由于粗心，他算错了其中一个y值，则这个错误的数值是（　　）

    A. －11 B. －5 C. 2 D. －2

    B 【解析】由函数图象关于对称轴对称，得（-1，-2），（0，1），（1，-2）在函数图象上， 把（-1，-2），（0，1），（1，-2）代入函数解析式，得 ， 解得 ， 则函数解析式为：y=-3x²+1， 当x=±2时，y=-11，故错误的数值是-5. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：广东省揭阳市揭西县2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

    计算： =_____________。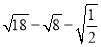

    【解析】根据二次根式的性质和二次根式的化简，可知==. 故答案为： .

    查看答案和解析>>

    科目：初中数学 来源：北京市顺义区2017-2018学年度第一学期期末教学质量检测八年级数学试卷 题型：解答题

    在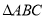中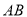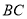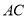， ， ， 三边的长分别为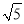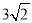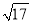， ， ，求这个三角形的面积.

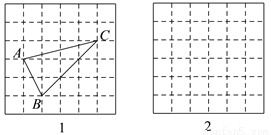
    小明同学在解答这道题时，先建立了一个正方形网格（每个小正方形的边长为1），再在网格中

    画出格点△ABC中，（即△ABC三个顶点都在小正方形的顶点处），如图1所示，这样不需要△ABC高，借用网格就能计算出它的面积.

    （1）△ABC的面积为 ；

    （2）如果△MNP三边的长分别为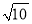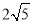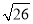， ， ，请利用图2的正方形网格（每个小正方形的边长为1）画出相应的格点△MNP，并直接写出△MNP的面积为 .

    （1）4.5；（2）作图见解析，7. 【解析】试题分析：（1）根据网格图结合割补法可得：S△ABC=S矩形MONC－S△CMA－S△AOB－S△BNC=12－2－1－4.5=4.5；（2）利用割补法可得：S△MNP=S矩形BMOA－S△BMP－S△MON－S△ANP= 15－1.5－2.5－4=7. 试题解析： （1） S△ABC=S矩形MONC－S△CMA－S△AOB－S...

    查看答案和解析>>

    同步练习册答案