
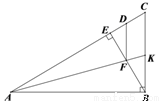
如图,在△ABC中,∠ABC=90°,BE⊥AC于点E,点D在AC上,且AD=AB,AK平分∠CAB,交线段BE于点F,交边CB于点K.
(1)在图中找出一对全等三角形,并证明;
(2)求证:FD∥BC .
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级北师大版数学试卷(C卷) 题型:单选题
如图,用平面去截圆锥,所得截面的形状是( )
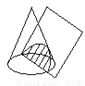
A. 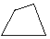 B.
B.  C.
C. 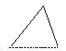 D.
D. 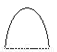
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 小题好拿分 题型:单选题
若分式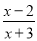 有意义,则
有意义,则 的取值范围是
的取值范围是
A. 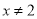 B.
B. 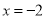 C.
C. 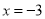 D.
D. 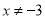
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
先阅读第(1)题的解答过程,然后再解第(2)题.
(1)已知多项式2x3﹣x2+m有一个因式是2x+1,求m的值.
解法一:设2x3﹣x2+m=(2x+1)(x2+ax+b),则:2x3﹣x2+m=2x3+(2a+1)x2+(a+2b)x+b
比较系数得:  ,解得:
,解得: 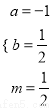 ,∴
,∴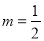 .
.
解法二:设2x3﹣x2+m=A•(2x+1)(A为整式)
由于上式为恒等式,为方便计算了取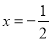 ,
, 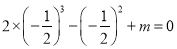 ,故
,故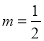 .
.
(2)已知x4+mx3+nx﹣16有因式(x﹣1)和(x﹣2),求m、n的值.
m=﹣5,n=20. 【解析】试题分析: 仔细阅读题文中第(1)部分的内容,理解解题思想方法;然后参照(1)的方法:设x4+mx3+nx﹣16=A(x﹣1)(x﹣2),对x进行两次赋值,可得出两个关于m、n的方程,联立求解可得出m、n的值. 试题解析: 设x4+mx3+nx﹣16=A(x﹣1)(x﹣2)(A为整式),取x=1,得1+m+n﹣16=0①;取x=2,得16+8m...查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
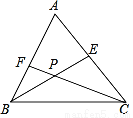
如图,在△ABC中,∠ABC和∠ACB的平分线BE、CF相交于点P.
(1)若∠ABC=70°,∠ACB=50°,则∠BPC= °;
(2)求证:∠BPC=180°﹣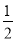 (∠ABC+∠ACB);
(∠ABC+∠ACB);
(3)若∠A=α,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016-17学年度第一学期期末教学质量检测七年级数学试卷 题型:解答题
春节将至,市区两大商场均推出优惠活动:
①商场一全场购物每满100元返30元现金(不足100元不返);
②商场二所有的商品均按8折销售.
某同学在两家商场发现他看中的运动服的单价相同,书包的单价也相同,这两件商品的单价之和为470元,且运动服的单价是书包的单价的7倍少10元.
(1)根据以上信息,求运动服和书包的单价.
(2)该同学要购买这两件商品,请你帮他设计出最佳的购买方案,并求出他所要付的费用.
(1)设书包的单价为60元,运动服的单价为410元; (2)他应在商场一购买运动服,在商场二购买书包,此时所付的费用为338元. 【解析】试题分析:(1)利用运动服的单价是书包的单价的7倍少10元,可设书包单价为x元,则运动服的单价为(7x-10)元,然后根据价格和列方程,再解方程求出x和7x-10即可; (2)商场二商品八折销售,则470元的价格实际费用为470×0.8;商场一...查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016-17学年度第一学期期末教学质量检测七年级数学试卷 题型:解答题
计算:(?1)2013×| ?3 |?(?2)3+4÷(?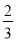 )2
)2
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
如图所示,已知 是⊙
是⊙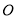 的直径,
的直径, 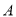 、
、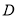 是⊙
是⊙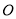 上的两点.
上的两点.

(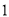 )若
)若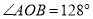 ,求
,求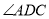 的度数.
的度数.
(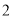 )已知
)已知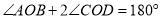 ,连接
,连接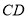 、
、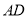 ,其中
,其中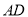 与直径
与直径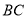 相交于点
相交于点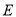 ,求证:
,求证: 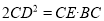 .
.
( )在(
)在(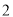 )的条件下,若
)的条件下,若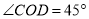 ,求
,求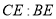 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:单选题
在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m3)是体积V(单位:m3)的反比例函数,它的图象如图所示,当V=10m3时,气体的密度是( )
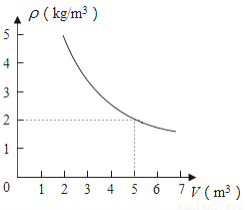
A. 5kg/m3 B. 2kg/m3 C. 100kg/m3 D. 1kg/m3
D 【解析】本题考查的是反比例函数的应用 先根据图象求出反比例函数关系式,即可求得当时,气体的密度。 设反比例函数关系式是, 图象过点(5,2) ,解得, 反比例函数关系式是, 当时,, 故选D。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com