
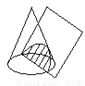
如图,用平面去截圆锥,所得截面的形状是( )
A. 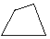 B.
B.  C.
C. 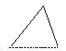 D.
D. 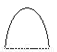
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源:2017年安徽省合肥市高新区梦园学校中考数学模拟试卷 题型:解答题
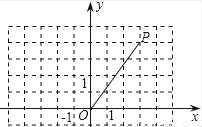
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
(1)在图中画出线段OP′;
(2)求P′的坐标和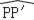 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 小题好拿分 题型:单选题
把8a3﹣8a2+2a进行因式分解,结果正确的是( )
A. 2a(4a2﹣4a+1) B. 8a2(a﹣1) C. 2a(2a﹣1)2 D. 2a(2a+1)2
C 【解析】试题分析:首先提取公因式2a,进而利用完全平方公式分解因式即可. 8a3﹣8a2+2a=2a(4a2﹣4a+1)=2a(2a﹣1)2.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级北师大版数学试卷(C卷) 题型:单选题
下列说法:①若a为任意有理数,则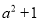 总是正数;②方程
总是正数;②方程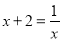 是一元一次方程;③若ab>0,a+b<0,则a<0,b<0;④
是一元一次方程;③若ab>0,a+b<0,则a<0,b<0;④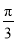 是分数;⑤单项式
是分数;⑤单项式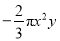 的系数是
的系数是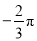 ,次数是4.其中错误的有( )
,次数是4.其中错误的有( )
A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】根据乘方的意义,可知a2≥0,因此a2+1>0,是正数,故①正确; 根据一元一次方程是整式方程,故②不正确; 根据ab>0,可知a、b同号,再由a+b<0,可知a<0、b<0,故③正确; 由于是无理数,故④不正确; 单项式的系数是,故⑤正确. 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级北师大版数学试卷(C卷) 题型:单选题
如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“S”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
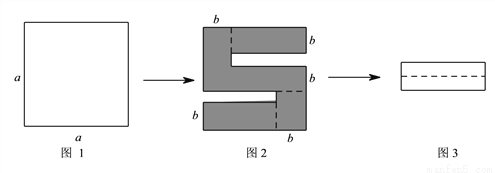
A. 4a-8b B. 2a-3b C. 2a-4b D. 4a-10b
A 【解析】根据图示可知新长方形的长为a-2,宽为a-3b,可得周长=2(长+宽)=2[(a-b)+(a-3b)]=4a-8b. 故选:A.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级北师大版数学试卷(A卷) 题型:解答题
化简并求值:
(1)5(3a2b﹣ab2)﹣(ab2+3a2b),其中a=﹣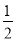 ,b=
,b=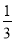 .
.
(2)已知|x+1|+(y﹣2)2=0,求(2x2y﹣2xy2)﹣[(3x2y2+3x2y)+(3x2y2﹣3xy2)]的值.
(1), ;(2)-30. 【解析】试题分析:(1)先去括号,然后合并同类项,再把数值代入进行求值即可; (2)先对所求式子进行化简,然后根据|x+1|+(y﹣2)2=0求出x、y的值,最后再代入进行求值即可. 试题解析:(1)原式= =, 当时,原式==; (2)(2x2y﹣2xy2)﹣[(3x2y2+3x2y)+(3x2y2﹣3xy2)] =2x2y-2xy...查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级北师大版数学试卷(A卷) 题型:填空题
请写出一个所含字母只有x、y,且二次项系数和常数项都是-5的三次三项式:________________________.
答案不唯一,如x3―5xy―5 【解析】利用多项式的项数和次数的定义写出一个满足条件的多项式即可. 【解析】 所有字母只有x,y,且二次项系数和常数项都是-5的三次三项式可为x3-5xy-5. 故答案为:x3-5xy-5.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 小题好拿分 题型:填空题
分解因式:ax2﹣2a2x+a3=_____________ .
a(x﹣a)2 【解析】原式=a(x2﹣2ax+a2)=a(x﹣a)2.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
如图,在△ABC中,∠ABC=90°,BE⊥AC于点E,点D在AC上,且AD=AB,AK平分∠CAB,交线段BE于点F,交边CB于点K.
(1)在图中找出一对全等三角形,并证明;
(2)求证:FD∥BC .
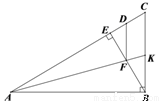
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com