练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若关于x的一元一次不等式组的解集是x＜5，则m的取值范围是（　　）

    A. m≥5 B. m＞5 C. m≤5 D. m＜5

    A 【解析】解不等式2x-1＞3（x-2）可得x＜5，然后由不等式组的解集为x＜5，可知m≥5. 故选：A.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级下册 第一章 整式的乘除 1.6完全平方公式 同步测试 题型：单选题

    下列计算正确的是（　　）

    A. （x+y）2=x2+y2 B. （x﹣y）2=x2﹣2xy﹣y2

    C. （x+1）（x﹣1）=x2﹣1 D. （x﹣1）2=x2﹣1

    C 【解析】试题分析：根据完全平方公式可得选项A，（x+y）2=x2+y2+2xy，故此选项错误；选项B，（x﹣y）2=x2﹣2xy+y2，故此选项错误；选项D，（x﹣1）2=x2﹣2x+1，故此选项错误；根据平方差公式可得选项C，（x+1）（x﹣1）=x2﹣1，故此选项正确；故答案选C．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018河北省保定市莲池区七年级第一学期数学期末试卷 题型：单选题

    有一个盛有水的圆柱体玻璃容器，它的底面半径为10cm，容器内水的高度为12cm，把一根半径为2cm的玻璃棒垂直插入水中，容器里的水升高了（　　）

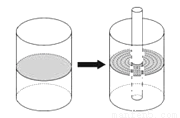
    A. 2cm B. 1.5cm C. 1cm D. 0.5cm

    D 【解析】设容器内的水将升高xcm，根据等量关系“容器的底面积×容器中水的原来高度+玻璃棒的截面积×（容器中水的高度+水增加的高度）=容器的底面积×（容器中水原来的高度+水增加的高度）”，可列方程π•102×12+π•22（12+x）=π•102（12+x），解得x=0.5．所以容器内的水将升高0.5cm．故选D.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018 北师大版数学八年级下册 第二章 一元一次不等式和一元一次不等式组 单元检测卷 题型：解答题

    已知关于x的不等式组有解，求实数a的取值范围，并写出该不等式组的解集．

    a＜－6， ≤x＜－2. 【解析】试题分析：根据题意，分别求解两个不等式的解集，然后根据不等式有解求解a的取值范围，并写出不等式组的解集即可. 试题解析：解不等式3x－a≥0，得x≥， 解不等式 (x－2)＞3x＋4，得x＜－2， 由题意，得＜－2, 解得a＜－6， ∴不等式组的解集为≤x＜－2.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018 北师大版数学八年级下册 第二章 一元一次不等式和一元一次不等式组 单元检测卷 题型：填空题

    关于x的不等式组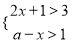的解集为1＜x＜3，则a的值为____．

    4 【解析】解不等式2x+1＞3可得x＞1，解不等式a-x＞1，可得x＜a-1，然后根据不等式组的解集为1＜x＜3，可知a-1=3，解得a=4. 故答案为：4.

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学 第二章 一元一次不等式与一元一次不等式组 单元检测卷 题型：解答题

    已知直线y=2x+b经过点（3，5），

    （1）求这个一次函数的解析式；

    （2）求关于x的不等式2x+b≥0的解集．

    （1）y=2x﹣1；（2）x≥ 【解析】试题分析：（1）将已知点的坐标代入直线的解析式求得b值即可确定其解析式； （2）直接解不等式即可． 试题解析：（1）∵直线y=2x+b经过点（3，5）， ∴2×3+b=5， 解得：b=﹣1， ∴直线的解析式为y=2x﹣1； （2）不等式为2x﹣1≥0， 解得：x≥．

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学 第二章 一元一次不等式与一元一次不等式组 单元检测卷 题型：填空题

    若关于x的不等式组的解表示在数轴上如图所示，则这个不等式组的解________ 

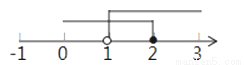
    1＜x≤2 【解析】由图示可看出，从1出发向右画出的折线且表示1的点是空心圆，表示x>1；从2出发向左画出的折线且表示2的点是实心圆，表示x≤2，所以这个不等式组的解集为1

    查看答案和解析>>

    科目：初中数学 来源：人教版初中数学七年级下册第八章《实际问题与二元一次方程组》同步练习 题型：解答题

    已知方程组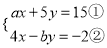，甲由于看错了方程①中的a，得到方程组的解为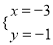，乙由于看错了方程②中的b，得到方程组的解为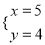，若按正确的a，b计算，求原方程组的解．

    . 【解析】试题分析： 由题意可知： 是方程的解， 是方程的解，由此可得： ，解此方程组即可求得正确的的值，代回原方程组，即可求得原方程组正确的解. 试题解析： 根据题意，得： ， 解得： ， 把， 分别代入原方程组，得， 由（1）×2+（2），得，解得： . 把代入（1），得.解得： ， ∴原方程组的解为： .

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：期中达标检测卷 题型：解答题

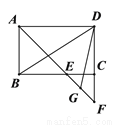
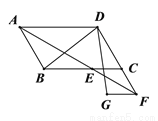
    在□ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F.

    （1）在图1中证明；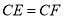

    （2）若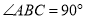，G是EF的中点（如图2），直接写出∠BDG的度数；

    （3）若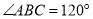，FG∥CE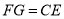， ，分别连结DB、DG（如图3），求∠BDG的度数.

    （1）证明见解析；（2）?BDG=45°.（3）?BDG=60°. 【解析】（1）根据AF平分∠BAD，可得∠BAF=∠DAF，利用四边形ABCD是平行四边形，求证∠CEF=∠F．即可 （2）根据∠ABC=90°，G是EF的中点可直接求得． （3）分别连接GB、GC，求证四边形CEGF是平行四边形，再求证△ECG是等边三角形．由AD∥BC及AF平分∠BAD可得∠BAE=∠AEB，...

    查看答案和解析>>

    同步练习册答案