
如图,延长平行四边形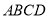 的边
的边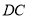 到点
到点 ,使
,使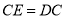 ,连接
,连接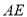 交
交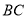 于点
于点 .
.
(1)求证: 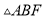 ≌
≌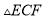 .
.
(2)连接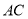 、
、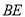 ,若
,若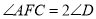 ,求证四边形
,求证四边形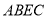 是矩形.
是矩形.
科目:初中数学 来源:吉林省长春市区2018届九年级上期末模拟数学试卷(解析版) 题型:填空题
若y=xm﹣2是二次函数,则m= .
4. 【解析】 试题分析:∵函数y=xm﹣2是二次函数,∴m﹣2=2,∴m=4. 故答案为4.查看答案和解析>>
科目:初中数学 来源:福建省三明市大田县2018届九年级(上)期中数学试卷(解析版) 题型:解答题
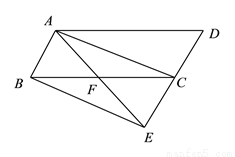
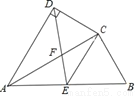
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,连接CE,连接DE交AC于F.
(1)求证:△ADC∽△ACB;
(2)若AD=4,AB=6,求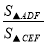 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:福建省三明市大田县2018届九年级(上)期中数学试卷(解析版) 题型:单选题
已知x:y=3:2,则下列各式中不正确的是( )
A. 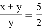 B.
B. 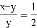 C.
C. 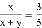 D.
D. 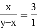
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(B卷) 题型:解答题
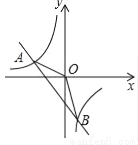
如图,一次函数y1=kx+b的图象与反比例函数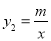 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
(1)试确定上述反比例函数和一次函数的表达式.
(2)求△AOB的面积.
(3)比较y1和y2的大小.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(B卷) 题型:填空题
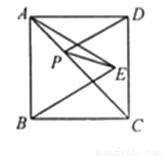
如图,正方形ABCD的面积为25, 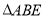 为等边三角形,点E在正方形ABCD内,若P是对角线AC上的一动点,则
为等边三角形,点E在正方形ABCD内,若P是对角线AC上的一动点,则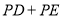 的最小值是__________.
的最小值是__________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(B卷) 题型:单选题
设x1、x2是方程x2+3x﹣3=0的两个实数根,则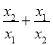 的值为( )
的值为( )
A. 5 B. ﹣5 C. 1 D. ﹣1
B 【解析】∵是关于的方程的两个根, ∴, , ∴. 故选B.查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级上期末模拟数学试卷(解析版) 题型:填空题
已知直角三角形两边x、y的长满足|x2-4|+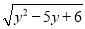 =0,则第三边长为 .
=0,则第三边长为 .
查看答案和解析>>
科目:初中数学 来源:2017-2018学年山东省诸城市 八年级上期末模拟数学试卷 题型:解答题
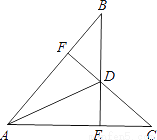
如图,BE⊥AC于E,CF⊥AB于F,CF、BE相交于点D,且BD=CD.求证:AD平分∠BAC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com