
设x1、x2是方程x2+3x﹣3=0的两个实数根,则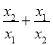 的值为( )
的值为( )
A. 5 B. ﹣5 C. 1 D. ﹣1
B 【解析】∵是关于的方程的两个根, ∴, , ∴. 故选B. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:吉林省长春市区2018届九年级上期末模拟数学试卷(解析版) 题型:单选题
已知二次函数y=a(x﹣2)2+c(a>0),当自变量x分别取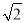 、3、0时,对应的函数值分别为y1、y2、y3 , 则y1、y2、y3的大小关系是( )
、3、0时,对应的函数值分别为y1、y2、y3 , 则y1、y2、y3的大小关系是( )
A. y1>y2>y3 B. y2>y1>y3 C. y3>y1>y2 D. y3>y2>y1
D 【解析】试题解析:∵a>0, ∴二次函数图象开口向上, 又∵对称轴为直线x=2, ∴x分别取时,对应的函数值分别为最小最大, 故选D.查看答案和解析>>
科目:初中数学 来源:福建省三明市大田县2018届九年级(上)期中数学试卷(解析版) 题型:单选题
关于x的方程m(x+h)2+k=0(m,h,k均为常数,m≠0)的解是x1=-3,x2=2,则方程m(x+h-3)2+k=0的解是( )
A. x1=-6,x2=-1 B. x1=0,x2=5 C. x1=-3,x2=5 D. x1=-6,x2=2
B 【解析】试题解析:解方程m(x+h)2+k=0(m,h,k均为常数,m≠0)得x=-h±, 而关于x的方程m(x+h)2+k=0(m,h,k均为常数,m≠0)的解是x1=-3,x2=2, 所以-h-=-3,-h+=2, 方程m(x+h-3)2+k=0的解为x=3-h±, 所以x1=3-3=0,x2=3+2=5. 故选:B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(B卷) 题型:解答题
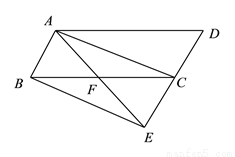
如图,延长平行四边形 的边
的边 到点
到点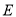 ,使
,使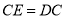 ,连接
,连接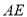 交
交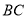 于点
于点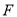 .
.
(1)求证: 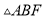 ≌
≌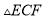 .
.
(2)连接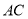 、
、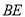 ,若
,若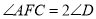 ,求证四边形
,求证四边形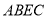 是矩形.
是矩形.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(B卷) 题型:单选题
如图,过双曲线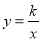 (k是常数,k>0,x>0)的图象上两点A,B分别作AC⊥x轴于C,BD⊥x轴于D,则△AOC的面积S1和△BOD的面积S2的大小关系为( )
(k是常数,k>0,x>0)的图象上两点A,B分别作AC⊥x轴于C,BD⊥x轴于D,则△AOC的面积S1和△BOD的面积S2的大小关系为( )
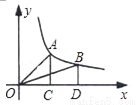
A. S1>S2 B. S1=S2
C. S1<S2 D. S1与S2无法确定
B 【解析】依题意可知,△AOC的面积S ₁和△BOD的面积S ₂有S ₁=S ₂=|k|. 故选B.查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级上期末模拟数学试卷(解析版) 题型:解答题
如图,四边形ABCD的对角线AC、BD相交于点O,分别作BE⊥AC于E,DF⊥AC于F,已知OE=OF,CE=AF.
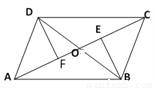
(1)求证:△BOE≌△DOF;
(2)若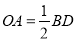 ,则四边形ABCD是什么特殊四边形?请说明理由.
,则四边形ABCD是什么特殊四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级上期末模拟数学试卷(解析版) 题型:填空题
在矩形纸片ABCD中,AB=16,AD=12,点P在边AB上,若将△DAP沿DP折叠,使点A恰好落在矩形对角线上的点A′处,则AP的长为________.
6或9 【解析】试题解析:①点A落在矩形对角线BD上,如图1所示: ∵AB=16,AD=12, ∴BD=20, 根据折叠的性质, 设AP=x,则BP=16?x, 解得:x=6, ∴AP=6; ②点A落在矩形对角线AC上,如图2所示: 由折叠的性质可知PD垂直平分AA′, ∴∠BAC=∠PDA. ∴tan∠BAC=tan∠PDA. ...查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级上期末模拟数学试卷(解析版) 题型:单选题
如图,在△ABC中,AB=15,AC=12,BC=9,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF长度的最小值是( )
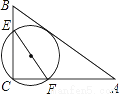
A. 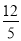 B.
B. 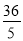 C.
C. 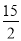 D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源:2017-2018学年山东省诸城市 八年级上期末模拟数学试卷 题型:填空题
小明随机调查了本班5名同学的家庭一个月的平均用水量(单位:t),记录如下:9,11,8,6,15,则这组数据的中位数是________ .
9 【解析】把数据按从小到大排列:6,8,9,11,15共有5个数,最中间一个数为9,所以这组数据的中位数为9, 故答案为:9.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com