
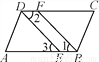
如图,已知∠ABC=∠ADC,BF,DE分别平分∠ABC与∠ADC,∠1=∠3,试说明:AB∥DC.
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:全册综合测试卷 题型:单选题
如果水库水位上升2m记作+2m,那么水库水位下降2m记作( )
A. -2 B. -4 C. -2m D. -4m
C 【解析】∵水位上升2m记作+2m, ∴水位下降2m记作-2m. 故选C.查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学 第17章 勾股定理 单元检测卷 题型:单选题
已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
A. 25 B. 14 C. 7 D. 7或25
D 【解析】试题分析:根据直角三角形的性质可得:第三边的平方=-=7或+=25.查看答案和解析>>
科目:初中数学 来源:广东省汕头市龙湖区2017-2018学年七年级上学期期末质量检测数学试卷 题型:单选题
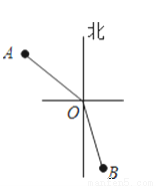
在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为( )
A. 69° B. 111° C. 141° D. 159°
C 【解析】试题分析:首先计算出∠3的度数,再计算∠AOB的度数即可. 【解析】 由题意得:∠1=54°,∠2=15°, ∠3=90°﹣54°=36°, ∠AOB=36°+90°+15°=141°, 故选:C.查看答案和解析>>
科目:初中数学 来源:广东省汕头市龙湖区2017-2018学年七年级上学期期末质量检测数学试卷 题型:单选题
过度包装既浪费资源又污染环境.据测算,如果全国每年减少10%的过度包装纸用量,那么可减排二氧化碳3120000吨,把数3120000用科学记数法表示为( )
A. 3.12×105 B. 3.12×106 C. 31.2×105 D. 0.312×107
B 【解析】由科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.因此3120000=3.12×106. 故选:B.查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第五章《平行线的性质与判定》同步练习(含答案) 题型:填空题
如图,要使 AD∥BF,则需要添加的条件是________(写一个即可)
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923292236627968/1924724835467264/STEM/5ecd4195ac4d4e9397f214c4de0469d1.png]
∠A=∠EBC 【解析】当∠ADC=∠DCF时,由内错角相等两直线平行可以得出AD∥BF; 故答案为∠ADC=∠DCF.查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第五章《平行线的性质与判定》同步练习(含答案) 题型:单选题
如图,点F,E分别在线段AB和CD上,下列条件能判定AB∥CD的是( )
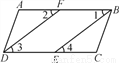
A. ∠1=∠2 B. ∠1=∠4 C. ∠4=∠2 D. ∠3=∠4
B 【解析】试题解析:A、∠1=∠2可以判定DF∥BE,故本选项错误; B、∠1=∠4,根据内错角相等,两直线平行,可以判定AB∥CD,故本选项正确; C、∠4=∠2能判定两直线平行,故本选项错误; D、∠3=∠4可以判定DF∥BE,故本选项错误; 故选B.查看答案和解析>>
科目:初中数学 来源:2016-2017学年北京市东城区七年级(上)期末数学试卷 题型:填空题
如图所示的框图表示解方程3﹣5x=4﹣2x的流程,其中“系数化为1”这一步骤的依据是_____.
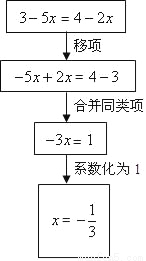
查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第五章《相交线与平行线--垂线》同步练习 题型:填空题
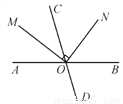
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com