练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知二次函数y=ax2+bx+c（a≠0，a、b、c为常数）的图象如图所示，下列5个结论：①abc＜0；②b＜a+c；③4a+2b+c＞0；④c＜4b；⑤a+b＜k（ka+b）（k为常数，且k≠1）．其中正确的结论有（   ）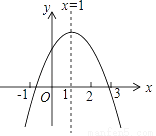

    A. 2个 B. 3个 C. 4个 D. 5个

    B 【解析】①由图象可知：a<0，c>0， ∵?>0，∴b>0，∴abc<0，故此选项正确； ②当x=?1时，y=a?b+c<0，∴b>a+b故b0，故此选项正确； ④当x=3时函数值小于0,y=9a+3b+c<0,且x=?=1，即a=?,代入得9(?)+3b+c<0,得c0，...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年七年级数学人教版5.1相交线同步练习 题型：解答题

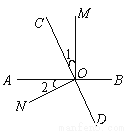
    如图,直线AB，CD相交于O点，OM⊥AB.

    （1）若∠1=∠2，求∠NOD；

    （2）若∠1=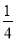∠BOC，求∠AOC与∠MOD.

    （1）90°；（2）∠AOC=60°，∠MOD＝150°. 【解析】（1）根据垂直的定义，可得∠AOC+∠1=90°由此易推出∠CON=90°，进而结合平角的定义即可解答本题； （2）根据垂直可知∠AOM=∠BOM=90°，结合∠1=∠BOC，可得∠1=30°，由此可以得到∠AOC与MOD的度数. 【解析】 （1）∵OM⊥AB， ∴∠AOM=90°，即∠AOC+∠1=90...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.2 探索直线平行的条件 同位角及平行公理 同步课堂练习题 题型：填空题

    直线l同侧有A、B、C三点，若A、B两点确定的直线l1与B、C两点确定的直线l2都与l平行，则A、B、C三点_____，其理论依据是_____________.

    共线 过直线外一点，有且只有一条直线与已知直线平行 【解析】由题意可知∥∥L,且直线与直线都经过点B，所以根据平行公理“过直线外一点，有且只有一条直线与已知直线平行”可得A. B. C三点共线。 故答案为：共线，过直线外一点，有且只有一条直线与已知直线平行.

    查看答案和解析>>

    科目：初中数学 来源：人教版2017-2018学年九年级下册数学全册综合测试卷 题型：填空题

    心理学家发现：学生对概念的接受能力y与提出概念的时间x（分）之间的关系式为y=﹣0.1x2+2.6x+43（0≤x≤30），若要达到最强接受能力59.9，则需________ 分钟．

    13 【解析】试题分析：直接代入求值即可． 试题解析：把y=59．9代入：y=-0．1x2+2．6x+43中得：x1=x2=13分钟． 即学生对概念的接受能力达到59．9时需要13分钟．

    查看答案和解析>>

    科目：初中数学 来源：人教版2017-2018学年九年级下册数学全册综合测试卷 题型：填空题

    若一个正比例函数的图象与一个反比例函数图象的一个交点坐标是（2，3），则另一个交点的坐标是________．

    （﹣2，﹣3） 【解析】∵反比例函数的图象与经过原点的直线的两个交点一定关于原点对称， ∴另一个交点的坐标与点(2,3)关于原点对称， ∴该点的坐标为(?2,?3). 故答案为：(?2,?3).

    查看答案和解析>>

    科目：初中数学 来源：人教版2017-2018学年九年级下册数学全册综合测试卷 题型：单选题

    如图，点N是反比例函数y=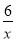（x＞0）图象上的一个动点，过点N作MN∥x轴，交直线y=﹣2x+4于点M，则△OMN面积的最小值是（   ）

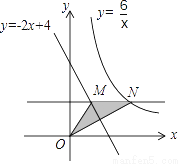
    A. 1                                            B. 2                                            C. 3                                            D. 4

    B 【解析】设点N的坐标为(,m),则点M的坐标为(4?2m,m)(m>0)， ∴MN=?(4?2m)=2m+?4， ∴S△OMN=MN?m=m2?2m+3=(m?1)2+2， ∴当m=1时，△OMN面积最小，最小值为2. 故选：B.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.2.1 用“同位角、第三直线”判定平行线 同步练习 题型：填空题

    如图,已知∠1=68°,∠2=68°,∠3=112°.

    (1)因为∠1=68°,∠2=68°(已知),

    所以∠1=∠2.

    所以_____________________∥_____________________ (同位角相等,两直线平行). 

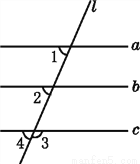
    (2)因为∠3+∠4=180°(平角的定义),∠3=112°,

    所以∠4=68°.

    又因为∠2=68°,

    所以∠2=∠4,

    所以_________________∥_________________ (同位角相等,两直线平行).

    (1)a;b (2)b;c 【解析】（1）求出∠1=∠2，根据平行线的判定推出： ∵∠1=68°，∠2=68°， ∴∠1=∠2， ∴直线a∥直线b， 故答案为：a，b； （2）求出∠4的度数，求出∠2=∠4，根据平行线的判定推出： ∵∠3+∠4=180°，3=112°， ∴∠4=68°， ∵∠2=68°， ∴∠2=∠4， ∴直线b∥直线c， 故答案为：b，c...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 全册综合测试卷1 题型：解答题

    某商场以每件280元的价格购进一批商品，当每件商品售价为360元时，每月可售出60件，为了扩大销售，商场决定采取适当降价的方式促销，经调查发现，如果每件商品降价1元，那么商场每月就可以多售出5件．要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品应降价多少元？

    要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品应降价60元． 【解析】试题分析：设每件商品应降价元，先表示出每件的利润．再乘以每月销售的数量，列方程求解即可. 【解析】 要使商场每月销售这种商品的利润达到 元，且更有利于减少库存，则设每件商品应降价元，由题意，得 解得： ∵有利于减少库存， 答：每件商品应降元.

    查看答案和解析>>

    科目：初中数学 来源：江苏省张家港市2017-2018学年第一学期初三数学期末考试试卷 题型：单选题

    已知：关于x的一元二次方程x2﹣（R+r）x+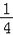d2=0有两个相等的实数根，其中R、r分别是⊙O1、⊙O2的半径，d为两圆的圆心距，则⊙O1与⊙O2的位置关系是( )

    A. 外离 B. 外切 C. 相交 D. 内含

    B 【解析】试题解析：由题中有两个相等的实数根可得， 即R+r=d，由圆与圆的位置关系判定法则可知，两圆的位置关系是外切. 故选B.

    查看答案和解析>>

    同步练习册答案