
��ͼ,��֪��1=68��,��2=68��,��3=112��.
(1)��Ϊ��1=68��,��2=68��(��֪),
���ԡ�1=��2.
����_____________________��_____________________ (ͬλ�����,��ֱ��ƽ��).
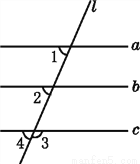
(2)��Ϊ��3+��4=180��(ƽ�ǵĶ���),��3=112��,
���ԡ�4=68��.
������2=68��,
���ԡ�2=��4,
����_________________��_________________ (ͬλ�����,��ֱ��ƽ��).
(1)a;b (2)b;c ����������1�������1=��2������ƽ���ߵ��ж��Ƴ��� �ߡ�1=68�㣬��2=68�㣬 ���1=��2�� ��ֱ��a��ֱ��b�� �ʴ�Ϊ��a��b�� ��2�������4�Ķ����������2=��4������ƽ���ߵ��ж��Ƴ��� �ߡ�3+��4=180�㣬3=112�㣬 ���4=68�㣬 �ߡ�2=68�㣬 ���2=��4�� ��ֱ��b��ֱ��c�� �ʴ�Ϊ��b��c...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ�˽̰�5.1�ཻ��ͬ����ϰ ���ͣ���ѡ��
�����ĸ�ͼ���У���1���2�ǶԶ��ǵ�ͼ�Σ� ��
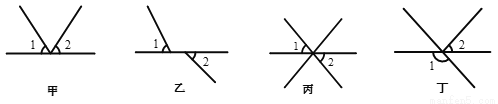
A. �� B. �� C. �� D. ��
C ��������������Ϊ�����ӳ��ߵ������ǽжԶ��ǣ����ݶ�����ͼ������жϼ��ɣ� �������� ������Ϊ�����ӳ��ߵ������ǽжԶ��ǣ� A.�����϶Զ��ǵĶ��壬�ʱ�ѡ����� B.�����϶Զ��ǵĶ��壬�ʱ�ѡ����� C.���϶Զ��ǵĶ��壬�ʱ�ѡ����ȷ�� D.�����϶Զ��ǵĶ��壬�ʱ�ѡ����� ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰�2017-2018ѧ����꼶�²���ѧȫ���ۺϲ��Ծ� ���ͣ������
��֪���κ���y=2x2��2�ͺ���y=5x+1��
��1��������ͼ���������2x2��2=5x+1�Ľ������Կ���
��2����ͨ���ⷽ�̵ķ�����֤��1���ʵĽ⣮
x1=����x2=3�� �������������������1�����ݺ���ͼ��Ľ�����������Ӧ���̵Ľ⣬�ɵô𰸣� ��2��������ʽ�ֽ⣬�ɵ÷��̵Ľ⣮ �����������1����ͼ��ƽ��ֱ������ϵ�ڻ���y=2x2��2�ͺ���y=5x+1��ͼ�� ͼ��ĺ������ǩ���3�� ����2x2��2=5x+1�Ľ���x1=����x2=3�� ��2�������2x2��5x��3=0�� ��ʽ�ֽ⣬�ã�2x+1����...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰�2017-2018ѧ����꼶�²���ѧȫ���ۺϲ��Ծ� ���ͣ���ѡ��
��֪���κ���y=ax2+bx+c��a��0��a��b��cΪ��������ͼ����ͼ��ʾ������5�����ۣ���abc��0����b��a+c����4a+2b+c��0����c��4b����a+b��k��ka+b����kΪ��������k��1����������ȷ�Ľ����У� �� 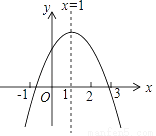
A. 2�� B. 3�� C. 4�� D. 5��
B ������������ͼ���֪��a<0��c>0�� ��?>0����b>0����abc<0���ʴ�ѡ����ȷ�� �ڵ�x=?1ʱ��y=a?b+c<0����b>a+b��b�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰�2017-2018ѧ����꼶�²���ѧȫ���ۺϲ��Ծ� ���ͣ���ѡ��
���κ���y=-x2+2x+2��Ϊy=a��x-h��2+k����ʽ��������ȷ����( )
A. y=-��x-1��2+2 B. y=-��x-1��2+3 C. y=��x-2��2+2 D. y=��x-2��2+4
B ���������������Ĺؼ���ʹ���䷽�����ɵö���ʽ��������ʽ. �������� y=x2-2x+4�䷽���� y=��x-1��2+3�� ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��2.2.1 �á�ͬλ�ǡ�����ֱ�ߡ��ж�ƽ���� ͬ����ϰ ���ͣ���ѡ��
��ͬһƽ���ڣ�ֱ��m��n�ཻ�ڵ�O����l��n����ֱ��l��m�Ĺ�ϵ��( )
A��ƽ��
B���ཻ
C���غ�
D�����϶��п���
B ����������ƽ�й����ɵã�ֱ��l��m������ƽ�У������O������ֱ����ֱ��lƽ�У���l��m�������غϣ�����l��m�ض��ཻ����ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��2.2.1 �á�ͬλ�ǡ�����ֱ�ߡ��ж�ƽ���� ͬ����ϰ ���ͣ���ѡ��
��ͼ��������ʶ�Ľ��У�ͬλ���ǣ�������
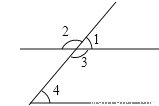
A. ��1�͡�2 B. ��1�͡�3 C. ��1�͡�4 D. ��2�͡�3
C ���������������������ͬλ�ǡ��ڲ��ǡ��Զ��ǵĶ�������жϣ� A����1�͡�2���ڲ��ǣ���A���� B����1�͡�3���ڲ��ǣ���B���� C����1�͡�4��ͬλ�ǣ���C��ȷ�� D����2�͡�3�ǶԶ��ǣ���D���� ��ѡC�� ����:ͬλ�ǡ��ڴ��ǡ�ͬ���ڽǣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ��ʦ����ϲ� ȫ���ۺϲ��Ծ�1 ���ͣ���ѡ��
������x��һԪ���η���(a��1)x2��2x��2=0��ʵ������������a�����ֵΪ�� ��
A. ��1 B. 0 C. 1 D. 2
B ����������Ϊ����x��һԪ���η���(a��1)x2��2x��2=0��ʵ����,����,��,���,��������a�����ֵΪ0,��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ�����м��� ���ͣ������
��ͼ����֪��A��P�ڷ���������y��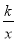 (k��0)��ͼ���ϣ���B��Q��ֱ��y��x��3��ͼ���ϣ���B��������Ϊ��1��AB��x�ᣬ��S��OAB��4����P��Q�������y��Գƣ����P������Ϊ(m��n)��
(k��0)��ͼ���ϣ���B��Q��ֱ��y��x��3��ͼ���ϣ���B��������Ϊ��1��AB��x�ᣬ��S��OAB��4����P��Q�������y��Գƣ����P������Ϊ(m��n)��
(1)���A�������k��ֵ��
(2)��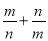 ��ֵ��
��ֵ��
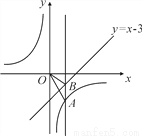
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com