练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若一个三角形的两边长分别为3和7，则第三边长可能是（ ）

    A．6 B．3 C．2 D．11

    A. 【解析】 试题分析：根据三角形三边关系，两边之和第三边，两边之差小于第三边可得4＜第三边长＜10，所以符合条件的整数为6，故答案选A．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年北师大七年级下1.5《平方差公式》练习题 题型：单选题

    计算：a2-(a+1)(a-1)的结果是( )

    A. 1 B. -1 C. 2a2+1 D. 2a2-1

    A 【解析】原式=，故选A.

    查看答案和解析>>

    科目：初中数学 来源：北师大七年级下1.7 整式的除法 同步练习含答案 题型：解答题

    已知2a-b=5,求[a2+b2+2b(a-b)-(a-b)2] ÷4b的值.

    . 【解析】试题分析：原式中括号中第二项利用单项式乘以多项式法则计算，第三项利用完全平方公式展开，去括号合并得到最简结果，再利用多项式除以单项式法则计算得到最简结果，然后将已知等式代入计算即可求出值． 解:原式=[a2+b2+2ab-2b2-(a2-2ab+b2)]÷4b =[a2+b2+2ab-2b2-a2+2ab-b2]÷4b=[4ab-2b2]÷4b =a-b= (2...

    查看答案和解析>>

    科目：初中数学 来源：北师大七年级下1.7 整式的除法 同步练习含答案 题型：单选题

    计算–12a6÷3a2的结果是（ ）

    A. –4a3 B. –4a8 C. –4a4 D. –a4

    C 【解析】-12a6÷3a2= -4a4. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型：单选题

    已知三角形的三边长为连续整数，且周长为12cm，则它的最短边长为（　　）

    A. 2cm B. 3cm C. 4cm D. 5cm

    B 【解析】试题解析：设大小处于中间的边长是xcm，则最大的边是(x+1)cm，最小的边长是(x?1)cm. 则(x+1)+x+(x?1)=12， 解得：x=4， 则最短的边长是：4?1=3cm. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型：单选题

    △ABC的三边长a,b,c满足关系式(a-b)(b-c)(c-a)=0,则这个三角形一定是(　　)

    A. 等腰三角形 B. 等边三角形 C. 等腰直角三角形 D. 无法确定

    A 【解析】∵(a-b)(b-c)(c-a)=0， ∴a-b=0或b-c=0或c-a=0， ∴a=b或b=c或c=a， 又∵a、b、c是△ABC的三边， ∴△ABC是等腰三角形. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型：单选题

    下列说法中正确的是(　　)

    A. 三角形的三条高都在三角形内 B. 直角三角形只有一条高

    C. 锐角三角形的三条高都在三角形内 D. 三角形每一边上的高都小于其他两边

    C 【解析】【解析】 三角形的高不一定在三角形内，故A错误； 任何三角形都有三条高，故B错误； 锐角三角形的三条高都在三角形内，正确； 直角三角形一条直角边的高等于另一条直角边，故D错误． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型：解答题

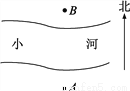
    如图所示的A、B是两根呈南北方向排列的电线杆，A、B之间有一条小河，小刚想估测这两根电线杆之间的距离，于是小刚从A点开始向正西方向走了20步到达一棵大树C处，接着又向前走了20步到达D处，然后他左转90°直行，当他看到电线杆B、大树C和他自己现在所处的位置E恰在同一条直线上时，他从D位置走到E处恰好走了100步，利用上述数据，小刚测出了A、B两根电线杆之间的距离．

    (1)请你根据上述的测量方法在原图上画出示意图；

    (2)如果小刚一步大约60厘米，请你求A、B两根电线杆之间的距离并简述理由．

    (1)图略 (2)AB＝60m 【解析】分析：（1）认真读题，根据题意画出示意图；（2）结合题意分别求出AC、DC、DE的长，易得：AC=DC，∠BAC=∠EDC，∠DCE=∠ACB，根据全等三角形的判定定理可得△ABC≌△DEC，进而得到AB=DE，据此，可得出结果. 本题解析：（1）根据题意画出图形，如图所示. （2）A、B两根电线杆之间的距离大约为36m.理由如下. ...

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

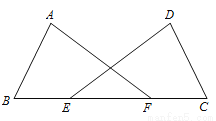
    如图，点E、F在BC上，BE=FC，AB=DC，∠B=∠C．求证：∠A=∠D．

    证明见解析． 【解析】试题分析：可通过证△ABF≌△DCE，来得出∠A=∠D的结论． 试题解析：∵BE=FC， ∴BE+EF=CF+EF， 即BF=CE； 又∵AB=DC，∠B=∠C， ∴△ABF≌△DCE；（SAS） ∴∠A=∠D．

    查看答案和解析>>

    同步练习册答案