
方程x2=2x的根为 .
x1=0,x2=2 【解析】试题分析:移项后分解因式,即可得出两个一元一次方程,求出方程的解即可. 【解析】 x2=2x, x2﹣2x=0, x(x﹣2)=0, x=0,或x﹣2=0, x1=0,x2=2, 故答案为:x1=0,x2=2. 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源:山东省2018届九年级上学期第二次月考数学试卷 题型:单选题
如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( )
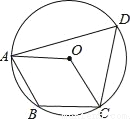
A. 45° B. 50° C. 60° D. 75°
C 【解析】设∠ADC的度数= ,∠ABC的度数= ,由题意可得,求出即可解决问题. 【解析】 设∠ADC的度数= ,∠ABC的度数= , ∵四边形ABCO是平行四边形, ∴∠ABC=∠AOC, ∵∠ADC= ,∠ADC= ,而, ∴, 解得: =120°,=60°,∠ADC=60°, 故选A. “点睛”该题主要考查了圆周角定理及其应用问题;...查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(华师大版):期末检测2 题型:填空题
不等式组 的解集是x>-1,则a的取值范围是______.
的解集是x>-1,则a的取值范围是______.
查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型:解答题
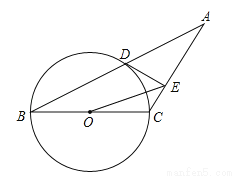
如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.
查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型:填空题
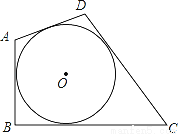
如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为_____.
查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型:单选题
如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=30°,CD=6,则圆的半径长为( )
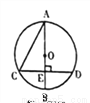
A. 2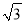 B. 2 C. 4
B. 2 C. 4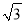 D.
D. 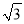
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sinα=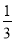 ,求sin2α的值.小娟是这样给小芸讲解的:
,求sin2α的值.小娟是这样给小芸讲解的:
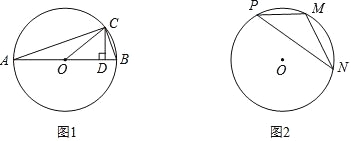
构造如图1所示的图形,在⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα=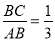 ,可设BC=x,则AB=3x,….
,可设BC=x,则AB=3x,….
【问题解决】
(1)请按照小娟的思路,利用图1求出sin2α的值;(写出完整的解答过程)
(2)如图2,已知点M,N,P为⊙O上的三点,且∠P=β,sinβ=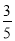 ,求sin2β的值.
,求sin2β的值.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型:填空题
如果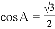 ,那么锐角A的度数为 .
,那么锐角A的度数为 .
查看答案和解析>>
科目:初中数学 来源:江苏省附属初级中学2017-2018学年八年级1月月考数学试卷 题型:解答题
求下列各式中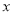 的值.
的值.
(1)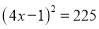 (2)
(2)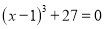
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com