
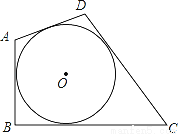
如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为_____.
科目:初中数学 来源:山东省2018届九年级上学期第二次月考数学试卷 题型:单选题
如图,在△ABC中,点D、E分别在边AB、AC上,如果DE∥BC,且∠DCE=∠B,那么下列说法中,错误的是( )
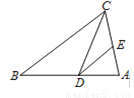
A. △ADE∽△ABC B. △ADE∽△ACD C. △ADE∽△DCB D. △DEC∽△CDB
C 【解析】试题解析:∵DE∥BC, ∴△ADE∽△ABC,∠BCD=∠CDE,∠ADE=∠B,∠AED=∠ACB, ∵∠DCE=∠B, ∴∠ADE=∠DCE, 又∵∠A=∠A, ∴△ADE∽△ACD; ∵∠BCD=∠CDE,∠DCE=∠B, ∴△DEC∽△CDB; ∵∠B=∠ADE, 但是∠BCD<∠AED,且∠BCD≠∠A, ∴...查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(华师大版):期末检测2 题型:解答题
解方程(组):
(1) 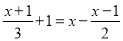 ; (2)
; (2) 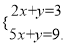
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(华师大版):期末检测2 题型:单选题
解方程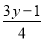 -1=
-1=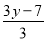 时,为了去分母,应将方程的两边同时乘( )
时,为了去分母,应将方程的两边同时乘( )
A. 12 B. 10 C. 9 D. 4
A 【解析】解方程时,为了去分母应将方程两边同时乘以12, 故选A查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型:解答题
在一个不透明的盒子里,装有三个分别写有数字1,2,3的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树形图或列表的方法,求下列事件的概率:
(1)两次取出小球上的数字相同的概率;
(2)两次取出小球上的数字之和大于3的概率.
(1) ;(2) 【解析】试题分析: (1)用列表法列出所有的等可能结果,观察表中数据即可求得两次取出小球上的数字相同的概率; (2)根据(1)中所列表格,找出两次数字之和大于3的所有结果,即可求得所求概率. 试题解析: (1)由题意,列表如下: 共有9种等可能的结果,并且它们出现的可能性相等, (1)两次取出小球上的数字相同的情况数有3种,分别是(1,1...查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型:填空题
方程x2=2x的根为 .
x1=0,x2=2 【解析】试题分析:移项后分解因式,即可得出两个一元一次方程,求出方程的解即可. 【解析】 x2=2x, x2﹣2x=0, x(x﹣2)=0, x=0,或x﹣2=0, x1=0,x2=2, 故答案为:x1=0,x2=2.查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型:单选题
向如图所示的地砖上随机地掷一个小球,当小球停下时,最终停在地砖上阴影部分的概率是( )

A. 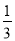 B.
B. 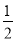 C.
C. 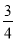 D.
D. 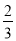
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型:填空题
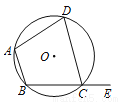
如图,四边形ABCD内接于⊙O,E是BC延长线上一点,若∠BAD=105°,则∠DCE的度数是_____°.
查看答案和解析>>
科目:初中数学 来源:江苏省附属初级中学2017-2018学年八年级1月月考数学试卷 题型:解答题
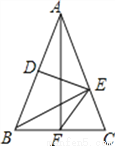
如图,在△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,
(1)求证:BF=EF;(2)求∠EFC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com