练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图,已知AE=AD,AB=AC,EC=DB,下列结论:

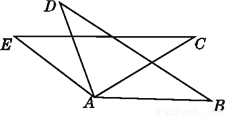
    ①∠C=∠B;②∠D=∠E;③∠EAD=∠BAC;④∠B=∠E.其中错误的是(　　)

    A. ①② B. ②③ C. ③④ D. 只有④

    D 【解析】因为AE＝AD，AB＝AC，EC＝DB； 所以△ABD≌△ACE(SSS)； 所以∠C＝∠B，∠D＝∠E，∠EAC=∠DAB； 所以 ∠EAC-∠DAC=∠DAB-∠DAC； 得∠EAD=∠CAB． 所以错误的结论是④，故选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级数学下4.3.3 用“边角边”判定三角形全等 同步练习 题型：解答题

    如图，△ABC和△ADE都是等腰三角形，且∠BAC=90°，∠DAE=90°，B，C，D在同一条直线上．求证：BD=CE．

    证明：∵△ABC和△ADE都是等腰直角三角形 ∴AD=AE AB=AC 又∵∠EAC=90°+∠CAD， ∠DAB=90°+∠CAD ∴∠DAB=∠EAC 在△ADB和△AEC中 ∴△ADB≌△AEC（SAS） 【解析】试题分析：求出AD=AE，AB=AC，∠DAB=∠EAC，根据SAS证出△ADB≌△AEC即可． 证明：∵△ABC和△ADE都是等腰直角三...

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第四章4.4用尺规作三角形课时练习 题型：单选题

    已知：∠AOB（图3-43）．

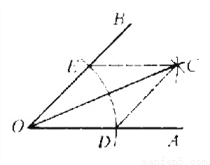
    作法：(1)在OA和OB上，分别截取OD、OE，使OD=OE．

    (2)分别以D、E为圆心，大于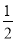DE的长为半径作弧，在∠AOB内，两弧交于点C．

    (3)作射线OC．

    OC就是所求的射线．

    这个作图是（ ）

    A. 平分已知角 B. 作一个角等于已知角 C. 作一个三角形等于已知三角形 D. 作一个角的平分线

    A 【解析】这个作图题属于基本作图中的平分已知角． 故选：A．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.1 三角形及其内角和 同步练习 题型：单选题

    在△ABC中，若∠A=95°，∠B=40°，则∠C的度数为（　　）

    A. 35° B. 40° C. 45° D. 50°

    C 【解析】试题分析：根据三角形的内角和是180°可知：∠A＋∠B＋∠C＝180°， ∴∠C＝180°－∠A－∠B ＝180°－95°－40° ＝45°． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.3.1 用“边边边”判定三角形全等 同步练习 题型：解答题

    如图,已知AB=AC,AD=AE,BD=CE,且B,D,E三点共线.试说明:∠3=∠1+∠2.

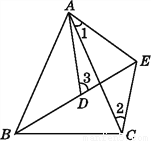
    见解析 【解析】分析：由AB=AC,AD=AE、BD=CE,可以得出△AEC全等△ADB，然后根据三角形全等和三角形外角的性质得出我们要求的角之间的关系. 本题解析：在△ABD和△ACE中, 所以△ABD≌△ACE. 所以∠BAD=∠1,∠ABD=∠2. 因为∠BAD+∠ABD+∠ADB=180°, ∠3+∠ADB=180°, 所以∠3=∠BAD+∠ABD...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.3.1 用“边边边”判定三角形全等 同步练习 题型：单选题

    如图,已知AC=FE,BC=DE,点A,D,B,F在一条直线上,要利用“SSS”证明△ABC≌△FDE,还可以添加的一个条件是(　　)

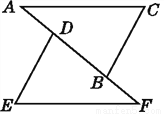
    A. AD=FB B. DE=BD C. BF=DB D. 以上都不对

    A 【解析】∵AC=FE，BC=DE， ∴要利用“SSS”证明△ABC≌△FDE，需添加条件“AB=DF”或“AD=BF”. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：2017年北师大七年级下1.5《平方差公式》练习题 题型：填空题

    观察下列各式：(a-1)(a+1)=a2-1，(a-1)(a2+a+1)=a3-1，(a-1)(a3+a2+a+1)=a4-1…根据前面各式的规律计算：(a-1)(a4+a3+a2+a+1)=_____；22012+22011+…+22+2+1=_____．

    a5-1 22013-1 【解析】观察题目中所给的算式可得(a-1)(a4+a3+a2+a+1)= a5-1； 22012+22011+…+22+2+1 =（2-1）（22012+22011+…+22+2+1） =2×（22012+22011+…+22+2+1）-（22012+22011+…+22+2+1） =22013+22012+22011+…+22+2-2201...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册4.3.2探索三角形全等的条件练习 题型：解答题

    已知，如图，△ABC中，AB=AC，动点D、E、F在AB、BC、AC上移动，移动过程中始终保持BD=CE，∠DEF=∠B，请你分析是否存在始终与△BDE全等的三角形，并说明理由。

    存在始终与△BDE全等的三角形，△CEF≌△BDE 【解析】分析：由三角形的外角性质和已知条件得出∠CEF=∠BDE，由等腰三角形的性质得出∠B=∠C，再由ASA证明△CEF≌△BDE即可． 本题解析： 存在始终与△BDE全等的三角形，△CEF≌△BDE；理由如下： ∵∠CED=∠B+∠BDE，∠DEF=∠B， ∴∠CEF=∠BDE， ∵AB=AC， ∴∠...

    查看答案和解析>>

    科目：初中数学 来源：北师大七年级下1.7 整式的除法 同步练习含答案 题型：解答题

    先化简,再求值:(2+a)(2-a)+a(a-5b)+3a5b3÷(-a2b)2,其中ab=-.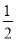

    5. 【解析】试题分析：本题考查了整式的化简求值，根据平方差公式，单项式乘以多项式，单项式除以单项式将所给多项式化简，然后代入求值. 解:原式=4-a2+a2-5ab+3a5b3÷a4b2=4-2ab. 当ab=-时,原式=4+2×=5.

    查看答案和解析>>

    同步练习册答案