练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

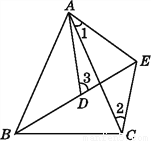
    如图,已知AB=AC,AD=AE,BD=CE,且B,D,E三点共线.试说明:∠3=∠1+∠2.

    见解析 【解析】分析：由AB=AC,AD=AE、BD=CE,可以得出△AEC全等△ADB，然后根据三角形全等和三角形外角的性质得出我们要求的角之间的关系. 本题解析：在△ABD和△ACE中, 所以△ABD≌△ACE. 所以∠BAD=∠1,∠ABD=∠2. 因为∠BAD+∠ABD+∠ADB=180°, ∠3+∠ADB=180°, 所以∠3=∠BAD+∠ABD...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级数学下4.3.3 用“边角边”判定三角形全等 同步练习 题型：解答题

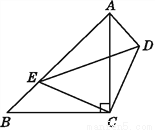
    如图,△ABC,△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上,试说明:△CDA≌△CEB.

    答案见解析 【解析】试题分析：根据等腰直角三角形的性质得出CE=CD，BC=AC，再利用全等三角形的判定证明即可． 试题解析：证明：∵△ABC、△CDE均为等腰直角三角形，∠ACB=∠DCE=90°， ∴CE=CD，BC=AC， ∴∠ACB﹣∠ACE=∠DCE﹣∠ACE， ∴∠ECB=∠DCA， 在△CDA与△CEB中， ， ∴△CDA≌△CEB．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第四章4.4用尺规作三角形课时练习 题型：单选题

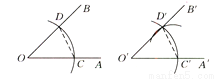
    用直尺和圆规作一个角等于已知角的示意图如图所示，则说明∠A′O′B′＝∠AOB的依据是 ( )

    A. SSS B. SAS C. ASA D. AAS

    A 【解析】根据用直尺和圆规作一个角等于已知角的示意图可知：OD=OD’,OC=OC’，CD=C’D’得 （SSS），得 . 故选A.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.1 三角形及其内角和 同步练习 题型：单选题

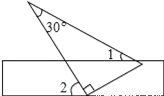
    如图，将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上．如果∠2=60°，那么∠1的度数为（　　）

    A. 60° B. 50° C. 40° D. 30°

    D 【解析】先根据直角三角板的性质得出∠AFE的度数，再根据平行线的性质求出∠2的度数即可． 【解析】 如图所示， ∵△GEF是含45°角的直角三角板， ∴∠GFE=45°， ∵∠1=25°， ∴∠AFE=∠GEF﹣∠1=45°﹣25°=20°， ∵AB∥CD， ∴∠2=∠AFE=20°． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.1 三角形及其内角和 同步练习 题型：填空题

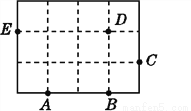
    如图,过A,B,C,D,E五个点中任意三点画三角形.

    (1)其中以AB为一边可以画出____________个三角形; 

    (2)其中以C为顶点可以画出____________个三角形. 

    3 6 【解析】试题分析：（1）以AB为一边可以画出3个三角形为：△ABE，△ABD，△ABC； （2）以C为顶点可以画出6个三角形为：△ABC，△BCD，△BCE，△ADC，△DEC，△ACE． 故答案为：（1）3；（2）6．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.3.1 用“边边边”判定三角形全等 同步练习 题型：单选题

    如图,已知AE=AD,AB=AC,EC=DB,下列结论:

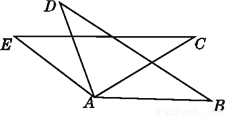
    ①∠C=∠B;②∠D=∠E;③∠EAD=∠BAC;④∠B=∠E.其中错误的是(　　)

    A. ①② B. ②③ C. ③④ D. 只有④

    D 【解析】因为AE＝AD，AB＝AC，EC＝DB； 所以△ABD≌△ACE(SSS)； 所以∠C＝∠B，∠D＝∠E，∠EAC=∠DAB； 所以 ∠EAC-∠DAC=∠DAB-∠DAC； 得∠EAD=∠CAB． 所以错误的结论是④，故选D.

    查看答案和解析>>

    科目：初中数学 来源：2017年北师大七年级下1.5《平方差公式》练习题 题型：解答题

    如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘 数”．如：4＝22-02，12＝42-22，20＝62-42，因此4，12，20这三个数都是神秘数．

    (1)28和2012这两个数是神秘数吗?为什么?

    (2)设两个连续偶数为2k+2和2k(其中k取非负整数)，由这两个连续偶数构造的神秘数是4的倍数吗?为什么?

    (3)两个连续奇数的平方差(取正数)是神秘数吗?为什么?

    (1)28和2012都是神秘数 (2)这两个连续偶数构造的神秘数是4的倍数(3)两个连续奇数的平方差不是神秘数． 【解析】试题分析： （1）将神秘数4开始，将一些神秘数写成如下的形式4=2×2＝22-02，12＝2×6＝42-22，20＝2×10＝62-42，…，则可判断28和2012这两个数是不是神秘数； （2）将这两个数平方相减，判断它们的差是不是4的倍数； （3）用n...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册4.3.2探索三角形全等的条件练习 题型：解答题

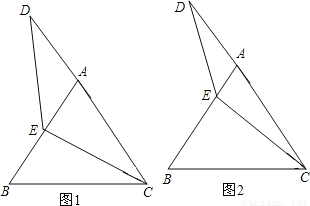
    等边△ABC中，点E在AB上，点D在CA的延长线上，且ED=EC．试探索以下问题：

    （1）如图1，当E为AB中点时，试确定线段AD与BE的大小关系，请你直接写出结论：AD BE；

    （2）如图2，若点E为线段AB上任意一点，（1）中结论是否成立，若成立，请证明结论，若不成立，请说明理由。

    （1）AD=BE；（2）证明见解析 【解析】分析：(1)根据题意易得∠D=∠AED=30°,即可得AD=AE,再根据AE=BE,即可解题; (2)通过作EF∥AC构造等边三角形把BE转化为EF,再利用“角角边”易证△AED≌△FCE,可得AD=FE,即可解题. 本题解析： （1）AD=BE； （2）过点E作EF∥AC交BC于点F， ∴∠EFB=∠ACB，∠BEF...

    查看答案和解析>>

    科目：初中数学 来源：北师大七年级下1.7 整式的除法 同步练习含答案 题型：解答题

    老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个二次三项式,形式如图:

    (1)求所捂的二次三项式;

    (2)若x=1,求所捂二次三项式的值.

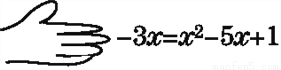
    （1）x2-2x+1.（2）0. 【解析】试题分析：（1）本题考查了整式的加减，根据被减数=差+减数列式计算即可；（2）把x=1代入（1）中所求出的式子计算求值. 解:(1)设所捂的二次三项式为A, 根据题意得A=x2-5x+1+3x=x2-2x+1. (2)当x=1时,原式=(x-1)2=(1-1)2=0.

    查看答案和解析>>

    同步练习册答案