
��֪����ͼ����ABC�У�AB=AC������D��E��F��AB��BC��AC���ƶ����ƶ�������ʼ�ձ���BD=CE����DEF=��B����������Ƿ����ʼ�����BDEȫ�ȵ������Σ���˵�����ɡ�


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�²������4.4�ó߹��������ο�ʱ��ϰ ���ͣ������
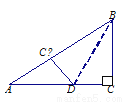
��ͼ����Rt��ABC�У���C��90�㣬AC��8��BC��6����ͼ����ʾ��������BCD��BD�۵���ʹ��C���ڱ�AB�ϵĵ�C�䴦�����ۺ�BD�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��4.3.1 �á��߱߱ߡ��ж�������ȫ�� ͬ����ϰ ���ͣ���ѡ��
��ͼ,��֪AE=AD,AB=AC,EC=DB,���н���:
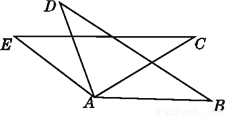
�١�C=��B;�ڡ�D=��E;�ۡ�EAD=��BAC;�ܡ�B=��E.���д������(����)
A. �٢� B. �ڢ� C. �ۢ� D. ֻ�Т�
D ����������ΪAE��AD��AB��AC��EC��DB�� ���ԡ�ABD�ա�ACE(SSS)�� ���ԡ�C����B����D����E����EAC=��DAB�� ���� ��EAC-��DAC=��DAB-��DAC�� �á�EAD=��CAB�� ���Դ���Ľ����Ǣܣ���ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�걱ʦ�����꼶��1.5��ƽ���ʽ����ϰ�� ���ͣ������
(x-y+z)��__________����z2-( x-y)2��
z-x+y ����������z2-( x-y)2=(z+x-y)(z-x+y),��(x-y+z) (z-x+y) ��z2-( x-y)2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶�²�4.3.2̽��������ȫ�ȵ�������ϰ ���ͣ������
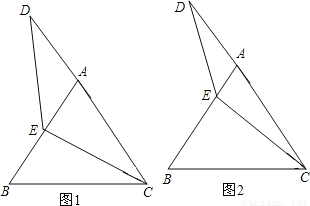
�ȱߡ�ABC�У���E��AB�ϣ���D��CA���ӳ����ϣ���ED=EC����̽���������⣺
��1����ͼ1����EΪAB�е�ʱ����ȷ���߶�AD��BE�Ĵ�С��ϵ������ֱ��д�����ۣ�AD BE��
��2����ͼ2������EΪ�߶�AB������һ�㣬��1���н����Ƿ����������������֤�����ۣ�������������˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶�²�4.3.2̽��������ȫ�ȵ�������ϰ ���ͣ���ѡ��
�ڡ�ABC�͡�EMN�У���֪��A=50�㣬��B=60�㣬��E=70�㣬��M=60�㣬AC=EN���������������Σ�������
A. һ��ȫ�� B. һ����ȫ�� C. ��һ��ȫ�� D. ���϶�����
A ���������ߡ�A=50�㣬��B=60�㣬 ���C=70�㣬 �ڡ�ABC�͡�NME�У� �� ���ABC�ա�NME(AAS)�� ��ѡA.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�²������3.1�ñ����ʾ�ı������ϵ��ʱ��ϰ ���ͣ������
Բ�����S��뾶R֮��Ĺ�ϵʽ��S=��R2�������Ա�����______��
R �����������ݺ����Ķ��壺���ں����е�ÿ��ֵR������S����һ���ķ�����һ��ȷ����ֵS��֮��Ӧ��֪R���Ա��������dz���. �ʴ�Ϊ��R���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�²������3.1�ñ����ʾ�ı������ϵ��ʱ��ϰ ���ͣ���ѡ��
����Բ���ܳ���ʽC=2��R������˵��������ǣ�������
A. ���DZ��� B. R��C�DZ��� C. R���Ա��� D. C�������
A ���������⣺A������һ���������dz�������ѡ��������⣻ B��R��C�DZ�������ѡ��������⣻ C��R���Ա�������ѡ��������⣻ D��C�����������ѡ��������⣮ ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��4.1.3 �����ε����ߡ���ƽ���� ͬ����ϰ ���ͣ������
��֪AD�ǡ�ABC�ĸ�,��BAD=72��,��CAD=21��,���BAC�Ķ���.
93��; 51�� ������������������ָ�AD�ڡ�ABC�ڲ����ⲿ�������������⼴�ɣ� ����������������� ����ͼ1������AD�ڡ�ABC���ڲ�ʱ����BAC=��BAD+��CAD=72��+21��=93�㣻 ����ͼ2������AD�ڡ�ABC���ⲿʱ����BAC=��BAD����CAD=72�㩁21��=51�㣮 ������������BAC�Ķ���Ϊ93���51�㣮�ʴ�Ϊ��93���51�㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com