
2014年索契冬奥会,大部分比赛将在总占地面积为142000平方米的“菲什特奥林匹克体育场”进行.将142000平方米用科学用科学记数法表示是_____平方米.
1.42×105 【解析】142000=1.42×105, 故答案为:1.42×105. 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源:山东省2017-2018学年八年级上期末模拟数学试卷 题型:单选题
下列条件中,不能判定△ABC是等腰三角形的是( )
A.a=3,b=3,c=4 B.a︰b︰c=2︰3︰4
C.∠B=50°,∠C=80° D.∠A︰∠B︰∠C=1︰1︰2
B 【解析】 试题分析:因为a=3,b=4,c=3,所以a=c,所以△ABC是等腰三角形,故A正确;因为a:b:c=2:3:4,所以a≠b≠c,所以△ABC不是等腰三角形,所以B错误;因为∠B=50°,∠C=80°,所以∠A=50°,所以∠A=∠B,所以△ABC是等腰三角形,所以C正确;因为∠A:∠B:∠C=1:1:2,所以∠A=∠B,所以△ABC是等腰三角形,所以D正确.故选:B. ...查看答案和解析>>
科目:初中数学 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:解答题
计算:
(1)2sin 30°+cos 60°-tan 60°·tan 30°+cos245°.
(2)| 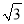 -5|+2·cos 30°+(
-5|+2·cos 30°+(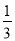 )-1+(9-
)-1+(9-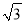 )0+
)0+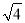
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:解答题
某饮料经营部每天的固定成本为200元,其销售的饮料每瓶进价为5元.销售单价与日平均销售的关系如下:
销售单价(元) | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | 9 |
日平均销售量(瓶) | 480 | 460 | 440 | 420 | 400 | 380 | 360 |
(1)若记销售单价比每瓶进价多x元,则销售量为_____(用含x的代数式表示);
求日均毛利润(日均毛利润=(每瓶售价-每瓶进价)×日均销售量-固定成本)y与x之间的函数关系式.
(2)若要使日均毛利润达到1400元,则销售单价应定为多少元?
(3)若要使日均毛利润达到最大,销售单价应定为多少元?最大日均毛利润为多少元?
(1)520﹣40x,y=﹣40x2+520x﹣200(0<x<13);(2)10元;(3)销售单价定为11.5元,日均毛利润达到最大值1490元. 【解析】试题分析: (1)观察表格中的数据可知,当销售价格每上涨0.5元时,销售量会减少20瓶,由此可得若记销售单价比每瓶进价多元,则销售量为: ,化简即可得所求答案;由日均毛利润=(每瓶售价-每瓶进价)×日均销售量-固定成本,列式即可得...查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:单选题
据兰州市旅游局最新统计,2014年春节黄金周期间,兰州市旅游收入约为11.3亿元,而2012年春节黄金周期间,兰州市旅游收入约为8.2亿元.假设这两年兰州市旅游收入的平均增长率为x,根据题意,所列方程为( )
A. 11.3(1﹣x%)2=8.2 B. 11.3(1﹣x)2=8.2 C. 8.2(1+x%)2=11.3 D. 8.2(1+x)2=11.3
D 【解析】设这两年兰州市旅游收入的平均增长率为x, 由题意得,8.2(1+x)2=11.3. 故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型:解答题
如图①,在平面直角坐标系中,二次函数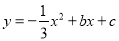 的图象与坐标轴交于
的图象与坐标轴交于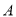 ,
, 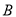 ,
, 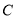 三点,其中点
三点,其中点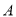 的坐标为
的坐标为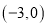 ,点
,点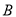 的坐标为
的坐标为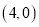 ,连接
,连接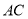 ,
, 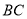 .动点
.动点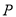 从点
从点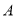 出发,在线段
出发,在线段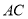 上以每秒
上以每秒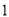 个单位长度的速度向点
个单位长度的速度向点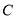 作匀速运动;同时,动点
作匀速运动;同时,动点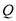 从点
从点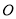 出发,在线段
出发,在线段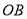 上以每秒
上以每秒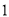 个单位长度的速度向点
个单位长度的速度向点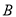 作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为
作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为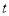 秒.连接
秒.连接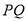 .
.
(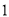 )填空:
)填空: 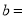 __________,
__________, 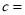 __________.
__________.
(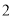 )在点
)在点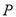 ,
, 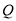 运动过程中,
运动过程中, 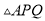 可能是直角三角形吗?请说明理由.
可能是直角三角形吗?请说明理由.
(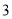 )在
)在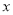 轴下方,该二次函数的图象上是否存在点
轴下方,该二次函数的图象上是否存在点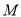 ,使
,使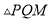 是以点
是以点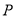 为直角顶点的等腰直角三角形?若存在,请求出运动时间
为直角顶点的等腰直角三角形?若存在,请求出运动时间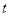 ;若不存在,请说明理由.
;若不存在,请说明理由.
(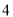 )如图②,点
)如图②,点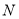 的坐标为
的坐标为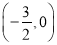 ,线段
,线段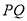 的中点为
的中点为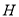 ,连接
,连接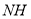 ,当点
,当点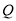 关于直线
关于直线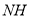 的对称点
的对称点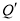 恰好落在线段
恰好落在线段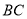 上时,请直接写出点
上时,请直接写出点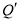 的坐标.
的坐标.
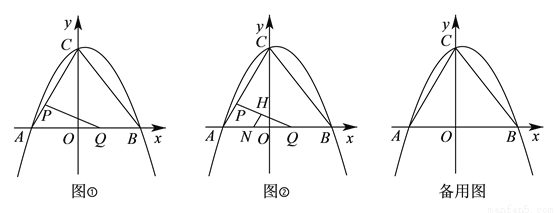
查看答案和解析>>
科目:初中数学 来源:2017年江苏省徐州市中考数学模拟试卷(2) 题型:解答题
(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
(1)原计划每天生产零件2400个,规定的天数是10天;(2)原计划安排的工人人数为480人. 【解析】试题分析:(1)设原计划每天生产零件x个,根据相等关系“原计划生产24000个零件所用时间=实际生产(24000+300)个零件所用的时间”可列方程,解出x即为原计划每天生产的零件个数,再代入即可求得规定天数;(2)设原计划安排的工人人数为y人,根据“(5组机器人生产流水线每天生产的零件个...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com