练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知∠A＝65°，则∠A的补角等于 ( )

    A. 125° B. 105° C. 115° D. 95°

    C 【解析】∵∠A=65°， ∴∠A的补角为180°-65°=115°， 故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖南省长沙市2017-2018学年九年级（上）第一次月考数学试卷 题型：解答题

    对平面直角坐标系中的点P（x，y），定义d=|x|+|y|，我们称d为P（x，y）的幸福指数．对于函数图象上任意一点P（x，y），若它的幸福指数d≥1恒成立，则称此函数为幸福函数，如二次函数y=x2+1就是一个幸福函数，理由如下：设P（x，y）为y=x2+1上任意一点，d=|x|+|y|=|x|+|x2+1|，∵|x|≥0，|x2+1|=x2+1≥1，∴d≥1．∴y=x2+1是一个幸福函数．

    （1）若点P在反比例函数y=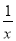的图象上，且它的幸福指数d=2，请直接写出所有满足条件的P点坐标；

    （2）一次函数y=﹣x+1是幸福函数吗？请判断并说明理由；

    （3）若二次函数y=x2﹣（2m+1）x+m2+m（m＞0）是幸福函数，试求出m的取值范围．

    （1）满足条件的P点坐标为（﹣1，﹣1）或（1，1）； （2）一次函数y=﹣x+1是幸福函数，理由见解析； （3）若二次函数y=x2﹣（2m+1）x+m2+m（m＞0）是幸福函数，m的取值范围为m≥2． 【解析】试题分析：（1）设点P的坐标为（m， ），根据幸福指数的定义，即可得出关于m的分式方程，解之经检验即可得出结论； （2）设P（x，y）为y＝－x＋1上的一点，分x＜...

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册 第1章 整式的乘除 章节检测题 题型：单选题

    下列运算正确的是( )

    A. a2＋a2＝a4 B. (－b2)3＝－b6 C. 2x·2x2＝2x3 D. (m－n)2＝m2－n2

    B 【解析】A. a²+a²=2a²，故本选项错误； B. （﹣b2）3=﹣b6，故本选项正确； C. 2x?2x²=4x³，故本选项错误； D. (m?n) ²=m²?2mn+n²，故本选项错误。 故选B.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.1.1 相交线与平行线 同步练习 题型：单选题

    如图,将一张长方形纸对折三次,则产生的折痕间的位置关系是(　　)

    A. 平行 B. 相交 C. 平行或相交 D. 无法确定

    C 【解析】试题解析：∵长方形对边平行， ∴根据平行公理，前两次折痕互相平行， ∵第三次折叠，是把平角折成两个相等的角， ∴是90°，与前两次折痕垂直． ∴折痕与折痕之间平行或垂直． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步练习题 含答案 题型：单选题

    如图，在所标识的角中，互为对顶角的两个角是（ ）

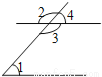
    A. ∠2和∠3 B. ∠1和∠3 C. ∠1和∠4 D. ∠1和∠2

    A 【解析】试题分析：两条直线相交后，所得的只有一个公共顶点，且两个角的两边互为反向延长线，这样的两个角叫做互为对顶角． 【解析】 根据同位角、同旁内角、邻补角、对顶角的定义进行判断， A、∠2和∠3是对顶角，正确； B、∠1和∠3是同旁内角，错误； C、∠1和∠4是同位角，错误； D、∠1和∠2的邻补角是内错角，错误． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步训练题 题型：解答题

    如图，P为∠BAC内一点，PE⊥AC于E，PF⊥AB于F，连接EF，并延长至D，若∠1＝∠2，判断∠PFE与∠PEF的大小关系，并说明理由．

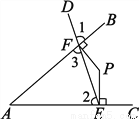
    ∠PFE＝∠PEF 【解析】试题分析：运用等角的余角相等即可求解. 试题解析：∠PFE＝∠PEF 理由如下：因为∠1＝∠3，∠1＝∠2，所以∠3＝∠2，又PF⊥AB，PE⊥AC，所以∠PFE＝∠PEF.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步训练题 题型：单选题

    如图，AD⊥BD，CD⊥BC，AB＝5cm，BC＝3cm，则线段BD的长度的取值范围是( )

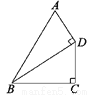
    A. 大于3cm B. 小于5cm C. 大于3cm且小于5cm D. 大于3cm或小于5cm

    C 【解析】试题解析：∵AD⊥BD，BC⊥CD，AB=5cm，BC=3cm， ∴BC＜BD＜AB， 即BD的长度的取值范围是大于3cm且小于5cm． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下1.4.3 多项式与多项式相乘 同步练习 题型：解答题

    计算:

    (1)(3x+2y)(9x2-6xy+4y2);

    (2)(3x-2y)(y-3x)-(2x-y)(3x+y).

    （1）27x3+8y3；（2）-15x2-y2+10xy 【解析】试题分析：用多项式乘多项式法则计算即可． 试题解析：解：(1)原式=27x3-18x2y+12xy2+18x2y-12xy2+8y3 =27x3+8y3； (2)原式=3xy-9x2-2y2+6xy-(6x2+2xy-3xy-y2) =-9x2-2y2+9xy-6x2+xy+y2 =-15x2-y...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下1.4.2 单项式与多项式相乘 同步练习 题型：解答题

    化简:

    (1)(-2ab)(3a2-2ab-4b2);

    (2)3x(2x-3y)-(2x-5y)·4x.

    (1) -6a3b+4a2b2+8ab3；(2) -2x2+11xy. 【解析】试题分析：（1）根据单项式乘多项式法则计算即可； （2）先用单项式乘多项式法则计算，然后合并同类项即可． 试题解析：【解析】 (1)原式=－6a3b+4a2b2+8ab3； (2)原式=6x2-9xy-8x2+20xy=－2x2+11xy．

    查看答案和解析>>

    同步练习册答案