练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列函数中，是二次函数的有（　　）

    ①y=1﹣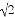x2②y=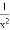③y=x（1﹣x）④y=（1﹣2x）（1+2x）

    A. 1个 B. 2个 C. 3个 D. 4个

    C 【解析】试题分析：①y=1-x2=-x2+1，是二次函数； ②y=，分母中含有自变量，不是二次函数； ③y=x（1-x）=-x2+x，是二次函数； ④y=（1-2x）（1+2x）=-4x2+1，是二次函数． 二次函数共三个，故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习（含答案） 题型：填空题

    方程x2﹣4=0的解是___________.

    x=2或-2 【解析】x2﹣4=0, (x-2)(x+2)=0, 所以x1=2，x2=-2.

    查看答案和解析>>

    科目：初中数学 来源：江苏省句容市片区合作共同体2017-2018学年年八年级上学期第二次学情测试数学试卷 题型：单选题

    下列四组线段中，可以构成直角三角形的是（    ）

    A. 4，5，6     B. 1.5，2，2.5    C. 2，3，4 D. 1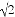，，3

    B 【解析】试题分析：根据勾股定理的逆定理，可知，可知不能构成直角三角形；由可知能够成直角三角形；由可知不能构成直角三角形；由可知不能构成直角三角形. 故选：B

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省中考数学模拟试卷 题型：单选题

    二次函数y=x2+bx的图象如图，对称轴为直线x=1，若关于x的一元二次方程x2+bx﹣t=0（t为实数）在﹣1＜x＜4的范围内有解，则t的取值范围是（　　）

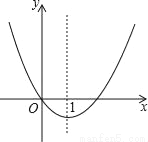
    A. t≥﹣1 B. ﹣1≤t＜3 C. ﹣1≤t＜8 D. 3＜t＜8

    C 【解析】试题分析：根据对称轴x==1，求出b的值为-2，从而得到x=﹣1、4时的函数值y分别为3、8，一元二次方程x2+bx﹣t=0（t为实数）在﹣1＜x＜4的范围内有解相当于y=x2+bx与y=t在x的范围内有交点的横坐标，如图所示，-1≤t＜8时，在﹣1＜x＜4的范围内有解． 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省中考数学模拟试卷 题型：单选题

    在一个不透明的布袋中，红色、黑色、白色的玻璃球共有60个，除颜色外，形状、大小、质地等完全相同．小刚通过多次摸球实验后发现其中摸到红色、黑色球的频率稳定在0.15和0.45，则口袋中白色球的个数很可能是（　　）个．

    A. 12 B. 24 C. 36 D. 48

    B 【解析】试题解析：∵小刚通过多次摸球实验后发现其中摸到红色、黑色球的频率稳定在0.15和0.45， ∴估计摸到红色、黑色球的概率分别为0.15和0.45， ∴摸到白球的概率为1-0.15-0.45=0.4， ∴口袋中白色球的个数为60×0.4=24， 即口袋中白色球的个数很可能24个． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年上学期苏州市初三数学期末综合检测 题型：解答题

    如图，在中，，是的中点，以为直径的⊙交的边于点、、.

    (1)求证:四边形是平行四边形;

    (2)若，求的度数.

    （1）见解析；（2）40° 【解析】试题分析：（1）连接DF，由直角三角形斜边上的中线性质得出BD=CD=AD，由圆周角定理可知DF⊥BC，证出DE∥BC，证明DE是△ABC的中位线，由三角形中位线定理得出DE=BC=BF，即可得出结论； （2）连接OG，由等腰三角形的性质得出∠DCA═∠A=35°，由三角形的外角性质得出∠ODG=∠A+∠DCA=70°，由等腰三角形的性质和三角形内角...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年上学期苏州市初三数学期末综合检测 题型：解答题

    解方程:

    (1) ;

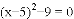    (2) 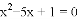(用配方法);

    (3)

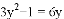
    (4)

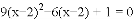
    (1) ； (2) ；(3) ；(4). 【解析】试题分析：（1）移项后两边开方，求出方程的解即可； （2）把常数项1移项后，应该在左右两边同时加上一次项系数-5的一半的平方； （3）利用配方法解方程； （4）设t=x-2，原方程转化为9t2-6t+1=0，通过解该方程求得t的值；然后代入来求x的值． 【解析】 (1)(x?5)2?9=0， (x?5)2=9，...

    查看答案和解析>>

    科目：初中数学 来源：山东省聊城市莘县2017-2018学年八年级（上）期中数学试卷 题型：解答题

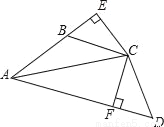
    如图，四边形ABCD中，∠ABC+∠D=180°，AC平分∠BAD，CE⊥AB，CF⊥AD．试说明：

    （1）△CBE≌△CDF；

    （2）AB+DF=AF．

    （1）证明见解析；（2）证明见解析. 【解析】试题分析：（1）根据角平分线的性质可得到CE=CF，根据余角的性质可得到∠EBC=∠D，已知CE⊥AB，CF⊥AD，从而利用AAS即可判定△CBE≌△CDF． （2）已知EC=CF，AC=AC，则根据HL判定△ACE≌△ACF得AE=AF，最后证得AB+DF=AF即可． 试题解析：证明：（1）∵AC平分∠BAD，CE⊥AB，CF⊥AD...

    查看答案和解析>>

    科目：初中数学 来源：安徽省亳州市利辛县2017-2018学年八年级上学期期中考试数学试卷 题型：单选题

    下列命题中，假命题是（ ）

    A. 三角形的一个外角大于任何一个不相邻的内角

    B. 三角形按边可分为不等边三角形、等腰三角形、等边三角形、

    C. 三角形中最少有2个锐角

    D. 三角形的三条中线交于一点，这个交点就是三角形的重心

    B 【解析】选项A、C、D为真命题；选项B， 三角形按边可分为不等边三角形、等腰三角形，等腰三角形又分腰和底边相等的等腰三角形和等边三角形，所以选项B 为假命题，故选B.

    查看答案和解析>>

    同步练习册答案