练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在同一坐标系中画出函数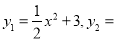 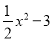和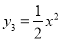的图象，并说明y1，y2的图象与函数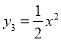的图象的关系．

    图略，y1，y2的图象是的图象分别向上和向下平移3个单位得到的 【解析】试题分析：根据描点法，可得函数图象，根据图象间的关系，可得答案． 试题解析：【解析】 如图，y1的图象由 图象向上平移3个单位得到； y2的图象由的图象向下平移3个单位得到．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版九年级数学上册 第23章 旋转 同步单元检测试卷（Word版附答案） 题型：解答题

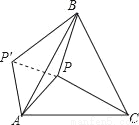
    如图，P是正三角形ABC内的一点，且PA=6，PB=8，PC=10，若将△PAC绕点A逆时针旋转后得到△P′AB．

    （1）求点P与点P′之间的距离；

    （2）求∠APB的大小．

    （1）6；（2）150° 【解析】试题分析：先根据等边三角形的性质得AB=AC，∠BAC=60°，再利用旋转的性质得∠P′AP=∠BAC=60°，AP′=AP，BP′=CP=13，于是可判断△AP′P为等边三角形，得到PP′=AP=5，∠APP′=60°，接着根据勾股定理的逆定理证明△BPP′为直角三角形，且∠BPP′=90°，然后利用∠APB=∠APP′+∠BPP′求出∠APB的度数． ...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年人教八年级数学上册 第14章 章末综合检测 题型：解答题

    计算：（1）992-102×98;

    （2）［x（x2y2-xy）-y（x2-x3y）］÷x2y.

    【答案】（1）-195（2）2xy-2

    【解析】试题分析：（1）利用平方差公式，完全平方公式简便计算.

    (2)提取公因式，化简.

    试题解析：

    （1）原式=（100-1）2-（100+2）×（100-2）

    =（1002-200+1）-（1002-4）=-200+5=-195.

    （2）原式=［x2y（xy-1）-x2y（1-xy）］÷x2y

    =2x2y（xy-1）÷x2y=2（xy-1）=2xy-2.

    【题型】解答题
    【结束】
    21

    （1）先化简，再求值：a（a-2b）+（a+b）2，其中a=-1，b=;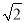

    （2）若x2-5x=3，求（x-1）（2x-1）-（x+1）2+1的值.

    （1）原式= 2a2+b2=2+2=4；（2）原式=4. 【解析】试题分析：(1)利用完全平方公式展开，化简，代入求值. (2) 利用完全平方公式展开，化简，整体代入求值. 解：（1）原式=a2-2ab+a2+2ab+b2=2a2+b2. 当a=-1，b=时，原式=2+2=4. （2）原式=2x2-3x+1-（x2+2x+1）+1=x2-5x+1=3+1=4.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年人教八年级数学上册 第14章 章末综合检测 题型：单选题

    把多项式x2+ax+b分解因式，得(x+1)(x－3)，则a，b的值分别是 （ ）

    A. a=2，b=3 B. a=－2，b=－3 C. a=－2，b =3 D. a=2，b=－3

    B 【解析】∵， ∴， 故选B.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.1.3二次函数ya（x-h）2+k的图象和性质（3）测试 题型：填空题

    将抛物线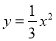向右平移3个单位，再向上平移2个单位，所得的抛物线的解析式为______．

    【解析】试题分析：抛物线的顶点坐标为（0，0），向右平移3个单位，再向上平移2个单位，所得的抛物线的顶点坐标为（3，2），根据顶点式可确定所得抛物线解析式． 试题解析：【解析】 依题意可知，原抛物线顶点坐标为（0，0），平移后抛物线顶点坐标为（3，2），又因为平移不改变二次项系数，所以所得抛物线解析式为： ，即．故答案为： ．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.1.3二次函数ya（x-h）2+k的图象和性质（3）测试 题型：填空题

    抛物线y＝3(x－2)2的开口方向是______，顶点坐标为______，对称轴是______．当x______时，y随x的增大而增大；当x＝______时，y有最______值是______，它可以由抛物线y＝3x2向______平移______个单位得到．

    向上 (2，0) 直线x＝ 2 ≥2 2 小 0 右 2． 【解析】【解析】 抛物线y＝3（x－2）2的开口方向是向上，顶点坐标为（2，0），对称轴是直线x＝ 2．当x≥2时，y随x的增大而增大；当x＝2时，y有最小值是0，它可以由抛物线y＝3x2向右平移2个单位得到． 故答案为：向上； （2，0）； 直线x＝ 2；≥2 ；2；小； 0； 右；2．

    查看答案和解析>>

    科目：初中数学 来源：人教版数学八年级上册 第11章 11.3.1 多边形同步练习（解析版） 题型：解答题

    在凸多边形中, 四边形有2条对角线, 五边形有5条对角线, 经过观察、探索、归纳, 你认为凸八边形的对角线条数应该是多少条? 简单扼要地写出你的思考过程.

    20 【解析】分析：将对角线的条数与凸多边形的边数进行关联，从边数少的凸多边形找出规律. 本题解析： 四边形有4个点，每个点可以画“(4-3)”条对角线，则一共“4×(4-3)=4”条对角线，这样每一条对角线算了两次，所以一共有“ ”条对角线； 同理，五边形有5个点，每个点可以画“(5-3)”条对角线，则一共“5×(5-3)=10”条对角线，这样每一条对角线算了两次，所以一...

    查看答案和解析>>

    科目：初中数学 来源：人教版数学八年级上册 第11章 11.3.1 多边形同步练习（解析版） 题型：单选题

    从五边形的一个顶点，可以引几条对角线（   ）

    A. 2 B. 3 C. 4 D. 5

    A 【解析】根据n边形从一个顶点出发可引出（n-3）条对角线可直接得到 从五边形的一个顶点可以引：5?3=2条对角线， 故选A.

    查看答案和解析>>

    科目：初中数学 来源：2016年秋八年级数学上册（人教版）11．2.2三角形的外角练习（附答案） 题型：

    已知等腰三角形的一个外角是120°,则它是( )

    A. 等腰直角三角形; B. 一般的等腰三角形; C. 等边三角形; D. 等腰钝角三角形

    C 【解析】①120°的角为顶角的外角，则顶角为180°-120°=60°，底角为（180°-60°）÷2=60°，三角形为等边三角形； ②120°的角为底角的外角，则底角为180°-120°=60°，顶角为180°-60°×2=60°，三角形为等边三角形． 故选C.

    查看答案和解析>>

    同步练习册答案