练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

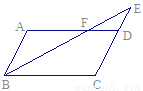
    如图，□ABCD中，E是CD的延长线上一点，BE与AD交于点F， ．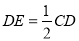

    （1）求证：△ABF∽△CEB；

    （2）若△DEF的面积为2，求□ABCD的面积．

    （1）证明见解析；（2）=24. 【解析】试题分析：（1）要证需找出两组对应角相等；已知平行四边形的对角相等，再利用，可得一对内错角相等，则可证； （2）由于，可根据两三角形的相似比，求出的面积，也就求出了四边形的面积．同理可根据，求出的面积，由此可求出的面积． 试题解析：（1）证明：∵四边形是平行四边形， ∴ （2）∵四边形是平行四边形， ∴ ， ， ，...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型：解答题

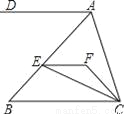
    如图，EF∥AD，AD∥BC，CE平分∠BCF，∠DAC=120°，∠ACF=20°，求∠FEC的度数．

    ∠FEC=20°． 【解析】试题分析：根据AD∥BC，∠DAC=120°可得:∠ACB=60°，根据∠ACF=20°可得：∠BCF=40°，根据角平分线的性质可得：∠BCE=20°，根据EF∥BC可得：∠FEC=∠BCE=20°.

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学全册综合测试卷 题型：填空题

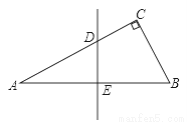
    如图，△ABC中，AB=AC，∠A=36°，AB的中垂线DE交AC于D，交AB于E，下述结论：（1）BD平分∠ABC；（2）AD=BD=BC；（3）△BDC的周长等于AB+BC；（4）D是AC中点．其中正确的命题序号是________ 

    （1）（2）（3） 【解析】根据线段垂直平分线的性质和等腰三角形ABC的顶角为36°，求出各角的度数，然后对各选项分析判断后利用排除法求解． 【解析】 ∵AB=AC，∠A=36°， ∴∠ABC=∠C=72°， ∵DE是AB的垂直平分线， ∴AD=BD，∠ABD=∠A=36°， ∴∠DBC=72°-36°=36°， ∠BDC=180°-36°-72°=72...

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学全册综合测试卷 题型：单选题

    如图，由∠1=∠2，∠D=∠B，推出以下结论，其中错误的是（ ）

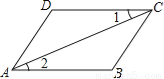
    A. AB∥DC B. AD∥BC C. ∠DAB=∠BCD D. ∠DCA=∠DAC

    D 【解析】【解析】 ∵∠1=∠2， ∴AB∥DC，故A选项结论正确； ∴∠D+∠BAD=180°，∠B+∠BCD=90°， ∵∠D=∠B， ∴∠B+∠BAD=180°，∠DAB=∠BCD，故C选项结论正确； ∴AD∥BC，故B选项结论正确； 只有AC平分∠BAD时，∠DCA=∠DAC，故D选项结论错误． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年度人教版九年级数学下册第26 章同步课时练习：26.2 实际问题与反比例函数（第2课时） 题型：解答题

    已知，二氧化碳气体的密度 ρ(kg／m 3)与体积 V(m 3)的反比例函数关系式是 ．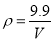

    （1）求当 V=5m 3时二氧化碳的密度 ρ；

    （2）请写出二氧化碳的密度 ρ随体积 V的增大（或减小）而变化的情况．

    （1）1.98；(2)二氧化碳的密度 ρ随体积 V的增大而减小． 【解析】试题分析： （1）把V=5m 3代入 即可求得对应的二氧化碳的密度ρ； （2）由“二氧化碳气体的密度 ρ(kg／m 3)与体积 V(m 3)满足函数关系式”可知，二氧化碳的密度 ρ随体积 V的增大而减小； 试题解析： （1）∵二氧化碳气体的密度 ρ(kg／m 3)与体积 V(m 3)满足函数关系...

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年度九年级（上）数学第一次月考试卷（11月份）(解析版) 题型：解答题

    如图，AD∥BC，∠ABC=90°，AB=8，AD=3，BC=4，点P为AB边上一动点，若△PAD与△PBC是相似三角形，求AP的长．

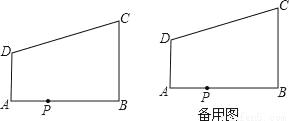
    AP=或AP=2或AP=6 【解析】试题分析:由AD//BC, ∠B=90°,可证∠PAD=∠PBC=90°, 又由AB=8,AD=3,BC=4,设AP的长为x,则BP长为8-x,然后分别从APD∽△BPC与△APD∽△BCP去分析,利用相似三角形的对应边成比例求解即可求得答案. 试题解析:∵ AB⊥BC, ∴ ∠B=90°, ∵ AD∥BC, ∴ ∠A=180°﹣∠...

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年度九年级（上）数学第一次月考试卷（11月份）(解析版) 题型：填空题

    已知Rt△ABC中，∠ACB=90°，AC=6，BC=8，点D是AB中点，点E是直线AC上一点，若以C、D、E为顶点的三角形与△ABC相似，则AE的长度为_____．

    3或 【解析】∵∠ACB=90°,AC=6,BC=8, ∴AB=62+82=10, ∵点D是AB中点, ∴CD=5, ∵CD=AD, ∴∠A=∠ACD, ∴C,D,E为顶点的三角形与△ABC相似，应分△ABC∽△CDE和△ABC∽△CED两种情况进行讨论: 当△ABC∽△CDE时: , 则,即CE=3,得到:AE=3, 当△ABC∽△CE...

    查看答案和解析>>

    科目：初中数学 来源：2018届九年级中考数学专题复习同步练习题：平行四边形 题型：解答题

    已知AC是菱形ABCD的对角线，∠BAC＝60°，点E是直线BC上的一个动点，连接AE，以AE为边作菱形AEFG，并且使∠EAG＝60°，连接CG，当点E在线段BC上时，如图1，易证：AB＝CG＋CE.

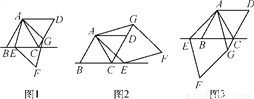
    (1)当点E在线段BC的延长线上时(如图2)，猜想AB，CG，CE之间的关系并证明；

    (2)当点E在线段CB的延长线上时(如图3)，直接写出AB，CG，CE之间的关系．

    (1)AB＝CG－CE(2)AB＝CE－CG 【解析】试题分析：（1）根据菱形的性质可得AC=AD，AE=AG，然后证明∠DAG=∠CAE，可利用SAS证明△ACE≌△ADG，根据全等三角形的性质可得CE=DG，再根据线段的和差关系和等量代换可得答案； （2）方法与（1）类似可证明△ACG≌△ABE，进而得到BE=CG，然后可得AB=CE﹣CG． 试题解析：(1)AB=CG-CE...

    查看答案和解析>>

    科目：初中数学 来源：江苏省无锡市2018届九年级上学期期末考试数学试卷 题型：单选题

    如图，半径为13 cm的圆形铁片上切下一块高为8 cm的弓形铁片，则弓形弦AB的长为( )

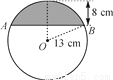
    A. 10 cm B. 16 cm

    C. 24 cm D. 26 cm

    C 【解析】试题分析：过O作OD⊥AB于C，交⊙O于D，先利用勾股定理求出BC的长，进而根据垂径定理得出AB. 【解析】 过O作OD⊥AB于C，交⊙O于D， ∴CD=8，OD=13， ∴OC=OD-CD=5， 又∵OB=13， ∴Rt△BCO中，BC==12， ∴AB=2BC=24． 故选C.

    查看答案和解析>>

    同步练习册答案