
已知等腰梯形的两条对角线互相垂直,中位线长为8cm,则它的面积为___cm2.
64 【解析】试题解析:过点O作OE⊥AB于E ∵AB∥CD ∴OE⊥CD于F ∵AC=BD,∠ADC=∠BCD,CD=DC ∴△ACD≌△BDC ∴∠ACD=∠BDC 又∵BD⊥AC ∴∠BDC=∠ACD=45° ∴OF=CD 同理可得OE=AB ∴EF=(AB+CD) 又∵中位线=(AB+CD)=8 ∴S梯形ABCD... 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷二 题型:填空题
已知圆锥的母线长为5cm,高为4cm,则该圆锥的侧面积为________cm2(结果保留π) 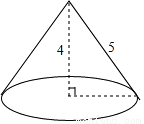
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷一 题型:填空题
已知抛物线y=﹣ x2﹣3x经过点(﹣2,m),那么m=________.
x2﹣3x经过点(﹣2,m),那么m=________.
查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试二 题型:解答题
如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4,设AB=x,AD=y,求x2+(y﹣4)2的值.
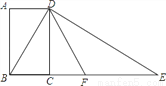
查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试二 题型:填空题
已知在△ABC中,AB=13cm,AC=15cm,高AD=12cm.则△ABC的周长为________.
42cm或32cm 【解析】 解:分两种情况求解: (1)当△ABC为锐角三角形时,在Rt△ABD中, , 在Rt△ACD中, , ∴BC=5+9=14, ∴△ABC的周长为:15+13+14=42cm; (2)当△ABC为钝角三角形时, BC=BD-CD=9-5=4, ∴△ABC的周长为:15+13+4=32cm;...查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试二 题型:单选题
如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,AD=1,则BD的长为( ) 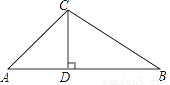
A. 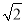 B. 2 C.
B. 2 C. 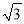 D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试二 题型:单选题
在?ABCD中,如果∠A+∠C=140°,那么∠C等于( )
A. 20° B. 40° C. 60° D. 70°
D 【解析】试题解析:如图, ∵四边形ABCD是平行四边形, ∴∠A=∠C, ∵∠A+∠C=140°, ∴2∠C=140°, ∴∠C=70°, 故选D.查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学第7-10章综合测试卷 题型:单选题
为了了解某市5万名初中毕业生的中考数学成绩,从中抽取500名学生的数学成绩进行统计分析,那么样本是( )
A. 某市5万名初中毕业生的中考数学成绩 B. 被抽取500名学生
C. 被抽取500名学生的数学成绩 D. 5万名初中毕业生
C 【解析】【解析】 样本是从总体中所抽取的一部分个体,故选C查看答案和解析>>
科目:初中数学 来源:北师大版数学九年级下册 1.1 锐角三角函数 题型:单选题
如图所示,在矩形ABCD中,DE⊥AC于E,设∠ADE=a,且cos a=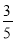 ,AB=4,则AD的长为 ( )
,AB=4,则AD的长为 ( )
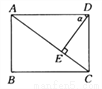
A. 3 B. 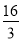 C.
C. 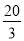 D.
D. 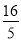
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com