练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在△ABC中，∠A=70°，∠B=55°，则△ABC是（　　）

    A. 钝角三角形 B. 等腰三角形

    C. 等边三角形 D. 等腰直角三角形

    B 【解析】【解析】 ∵在△ABC中，∠A=70°，∠B=55°，∴∠C=180°﹣∠A﹣∠B=55°，∴∠B=∠C，∴△ABC是等腰三角形．故选B．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：重庆市校2017-2018学年八年级上学期第二阶段考试数学试卷 题型：单选题

    如(x＋m)与(x＋3)的乘积中不含x的一次项，则m的值为（ ）

    A. 0 B. 3 C. －3 D. 1

    C 【解析】∵中不含的一次项， ∴， ∴. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 第24章小结与复习 测试 题型：单选题

    如图，CA为⊙O的切线，切点为A，点B在⊙O上，若∠CAB＝55°，则∠AOB等于(　　)

    A. 55° B. 90° C. 110° D. 120°

    C 【解析】因为CA为⊙O的切线，所以OA⊥AC，所以∠OAC=90°. 因为∠CAB=55°，所以∠OAB=90°-55°=35°， 因为OA=OB，所以∠OAB=∠B. 所以∠AOB=180°-2×35°=110°. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：湖北省大冶市金湖街办2017-2018学年八年级上学期第二次月考（12月）数学试卷 题型：填空题

    如图，在△ABC中，∠BAC＝90°，AB＝AC，∠BAD＝30°，AD＝AE，则∠EDC的度数是______．

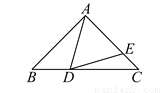
    15° 【解析】试题分析：先根据△ABC中，∠BAC=90°，AB=AC求出∠B=45°、∠DAE=60°，再根据AD=AE可得出∠AED=60°，由三角形内角和定理求出∠ADC=∠B+∠BAD=45°+30°=75°，进而可得∠EDC=∠ADC-∠ADE=75°-60°=15°．

    查看答案和解析>>

    科目：初中数学 来源：湖北省大冶市金湖街办2017-2018学年八年级上学期第二次月考（12月）数学试卷 题型：单选题

    若x2－2（k＋1）x＋4是完全平方式，则k的值为（  ）

    A. ±1 B. ±3 C. －1或3 D. 1或－3

    D 【解析】【解析】 ∵x2﹣2（k+1）x+4是完全平方式，∴x2﹣2（k+1）x+4=（x±2）2，∴﹣2（k+1）=±4，∴k1=﹣3，k2=1．故选D．

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

    如图6，已知箭头的方向是水流的方向，一艘游艇从江心岛的右侧A点逆流航行3小时到达B点后，又继续顺流航行2.5小时后到达C点，总共航行了208千米，已知水流的速度是2千米/时。

    （1）求游艇在静水中的速度。

    （2）由于AC段在建桥，游艇用同样的速度沿原路返回共需多少时间？（结果保留一位小数）

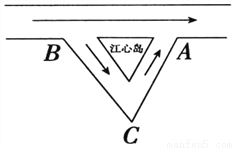
    （1）38千米/时；（2）5.5小时 【解析】试题分析：（1）游艇在静水中的速度为x千米/时，则顺流航行速度为（x+2）千米/时，逆流航行的速度为（x﹣2）千米/时，根据路程=速度×时间即可得出关于x的一元一次方程，解之即可得出结论； （2）根据路程=速度×时间分别算出AB、BC段的路程，再根据时间=路程÷速度即可得出返回所需时间． 试题解析：【解析】 （1）设游艇在静水中的速...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

    某地中国移动“全球通”与“神州行”收费标准如下表：

    品牌

    月租费

    本地话费（元/分钟）

    长途话费（元/分钟）

    全球通

    13元

    0.35

    0.15

    神州行

    0元

    0.60

    0.30

    如果小明每月拨打本地电话时间是长途电话时间的2倍，且每月总通话时间在65—70分钟之间，那么他选择_________较为省钱（填“全球通”或“神州行”）

    全球通 【解析】【解析】 设小明打长途电话的时间为x分钟，则打本地电话的时间为2x分钟，∴选择“全球通”所需总费用为13+0.15x+0.35×2x=0.85x+13，选择“神州行”所需总费用为0.3x+0.6×2x=1.5x，当0.85x+13＞1.5x，即0＜x＜20时，选择神州行较为省钱； 当0.85x+13=1.5x，即x=20时，都一样省钱； 当0.85x+13＜1....

    查看答案和解析>>

    科目：初中数学 来源：浙江省湖州市吴兴区2017-2018学年九年级上学期期末考试数学试卷 题型：解答题

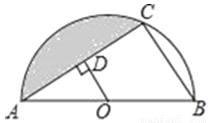
    如图，已知点O为半圆的圆心，直径AB=12，C是半圆上一点，OD⊥AC于点D，OD=3．

    （1）求AC的长；

    （2）求图中阴影部分的面积.

    (1) ;(2) . 【解析】试题分析：（1）根据垂径定理可知AD=DC，由OA=OB，推出BC=2OD=6，Z在Rt△ACB中，利用勾股定理求出AC． （2）首先证明△OBC设等边三角形，推出∠AOC=120°，根据S阴=S扇形OAC-S△AOC计算即可． 试题解析：（1）∵OD⊥AC， ∴ ∴AC=2AD= ， （2）连OC， 在Rt△ ADO中，∵O...

    查看答案和解析>>

    科目：初中数学 来源：2018春季学北师大版九年级数学下册期末测评试卷 题型：单选题

    如图，在平面直角坐标系中，抛物线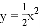经过平移得到抛物线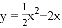，其对称轴与两段抛物线所围成的阴影部分的面积为

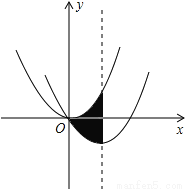
    A. 2 B. 4 C. 8 D. 16

    B 【解析】试题解析：过点C作CA⊥y， ∵抛物线y=x2-2x=（x2-4x）=（x2-4x+4）-2=（x-2）2-2， ∴顶点坐标为C（2，-2）， 对称轴与两段抛物线所围成的阴影部分的面积为：2×2=4， 故选B．

    查看答案和解析>>

    同步练习册答案