练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在平行四边形ABCD中，都不一定成立的是(　　) ①AO=CO；②AC⊥BD；③AD∥BC；④∠CAB=∠CAD．

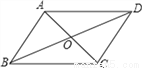
    A. ①和④ B. ②和③ C. ③和④ D. ②和④

    D 【解析】∵四边形ABCD是平行四边形， ∴AO=CO，故①成立； AD∥BC，故③成立； 利用排除法可得②与④不一定成立， ∵当四边形是菱形时，②和④成立。 故选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：上海市黄浦区2018届九年级上学期期末调研测试数学试卷（WORD版） 题型：填空题

    已知抛物线y=ax2+bx+c开口向上，一条平行于x轴的直线截此抛物线于M、N两点，那么线段MN的长度随直线向上平移而变_____．（填“大”或“小”）

    大 【解析】因为二次函数的开口向上,所以点M,N向上平移时,距离对称轴的距离越大,即MN的长度随直线向上平移而变大,故答案为:大.

    查看答案和解析>>

    科目：初中数学 来源：北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型：单选题

    已知：如图，D、E分别在AB、AC上，若AB=AC，AD=AE，∠A =60°，∠B=35°，则∠BDC的度数是( )

    A. 95° B. 90° C. 85° D. 80°

    A 【解析】【解析】 在△ABE和△ACD中，∵AE=AD，∠A=∠A，AB=AC，∴△ABE≌△ACD（SAS），∴∠C=∠B．∵∠B=35°，∴∠C=35°．∵∠A=60°，∴∠BDC=∠A+∠C=95°，故选A．

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省大庆市2016---2017学年度上期初三数学期末试卷 题型：填空题

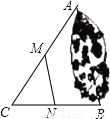
    如图，A，B两点被池塘隔开，在A，B外选一点C，连接AC和BC，并分别找出AC和BC的中点M，N，如果测得MM=20m，那么A，B两点间的距离是 ．

    40m． 【解析】 试题分析：根据三角形中位线定理：三角形的中位线平行第三边，且等于第三边的一半，那么第三边应等于中位线长的2倍．本题中，∵M，N分别是AC，BC的中点，∴MN是△ABC的中位线，∴MN=AB，∴AB=2MN=2×20=40（m）．

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省大庆市2016---2017学年度上期初三数学期末试卷 题型：单选题

    一次智力测验,有20道选择题.评分标准是:对1题给5分,错1题扣2分,不答题不给分也不扣分.小明有两道题未答.至少答对几道题,总分才不会低于60分.则小明至少答对的题数是( )

    A.11道 B。12题 C.13题 D.14题

    D 【解析】设小明至少答对的题数是x道， 5x-2（20-2-x）≥60， x≥135/7 ， 故应为14． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：浙江省余姚市2017-2018学年八年级上学期期中考试数学试卷 题型：解答题

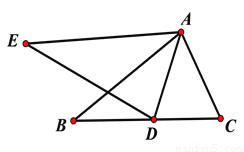
    如图，△AED的顶点D在△ABC的BC边上，∠E=∠B,AE=AB, ∠EAB=∠DAC.

    (1)求证：△AED≌△ABC.

    (2)若∠E=40°，∠DAC=30°，求∠BAD的度数.

    （1）证明见解析；（2）45° 【解析】分析：（1）易证∠EAD=∠BAC，再由已知条件即可证明△AED≌△ABC； （2））由△AED≌△ABC，推出AD=AC，∠B=∠E=40°，由∠DAC=30°，推出∠C=∠ADC=（180°-30°）=75°，由∠ADC=∠B+∠BAD，即可求出∠BAD． 本题解析： ∵∠EAB=∠DAC ∴∠EAB+∠BAD=∠DAC+∠...

    查看答案和解析>>

    科目：初中数学 来源：浙江省余姚市2017-2018学年八年级上学期期中考试数学试卷 题型：填空题

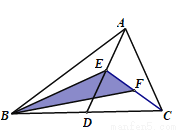
    如图所示，在△ABC中，已知点D、E、F分别为边BC、AD、CE的中点，且△ABC的面积是16cm2，则阴影部分的面积等于_______cm2．

    4 【解析】如图，∵E为AD的中点， ∴S△ABC:S△BCE=2:1， 同理可得, :=2:1， ∵S△ABC=16， ∴S△EFB=S△ABC=×16=4. 故答案为4.

    查看答案和解析>>

    科目：初中数学 来源：南京市玄武区2016~2017学年度第一学期期九年级试卷 题型：解答题

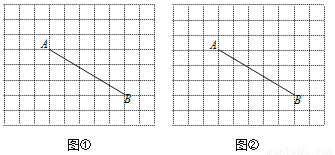
    如图，边长为1的小正方形组成了网格，点A、B均是格点，请你仅用无刻度的直尺画出满足下列条件的点P，并在图中标出点P．

    （1）图①中，点P在线段AB上且AP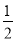＝AB；

    （2）图②中，点P在线段AB上且AP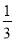＝AB．

    答案见解析． 【解析】分析：（1）如图1，连接CD与AB的交点为P，由 ,可得AP=AB，则点P即为所求作点；（2）如图2，连接EF交AB于点Q，由 ,可得AP=AB，则点P即为所求作点． 本题解析：（1）AP=AB，即P为AB中点， 如图所示，矩形对角线交点即为所求． （2）AP=AB，即，运用相似三角形．

    查看答案和解析>>

    科目：初中数学 来源：南京市溧水区2016~2017学年度第一学期期末九年级试卷 题型：填空题

    已知，则=_______________

    【解析】∵, ∴b= , ∴= .

    查看答案和解析>>

    同步练习册答案