
如图,已知点A在反比例函数y=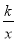 的图像上,点B在x轴的正半轴上,且△OAB是面积为
的图像上,点B在x轴的正半轴上,且△OAB是面积为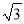 的等边三角形,那么这个反比例函数的解析式是( )
的等边三角形,那么这个反比例函数的解析式是( )
A. 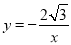 B.
B. 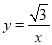 C.
C. 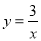 D.
D. 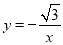
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:填空题
已知(x-y+3)2+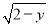 =0,则x+y=________.
=0,则x+y=________.
查看答案和解析>>
科目:初中数学 来源:青海省2017-2018学年七年级上学期12月月考数学试卷 题型:填空题
一个角的度数为33°52′,则这个角的余角为_______________
56°8′ 【解析】试题解析:根据余角的定义,这个角的余角为: 故答案为:查看答案和解析>>
科目:初中数学 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
如图,已知⊙O,用尺规作⊙O的内接正四边形ABCD.(写出结论,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
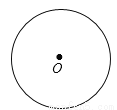
查看答案和解析>>
科目:初中数学 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:填空题
如图,某单位准备将院内一块长30m,宽20m的长方形花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图,要使种植花草的面积为532m2,设小道进出口的宽度为x m,根据条件,可列出方程:____________.
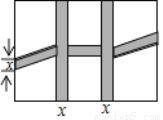
查看答案和解析>>
科目:初中数学 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:单选题
已知反比例函数y=-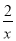 ,当x>0时,它的图象在( )
,当x>0时,它的图象在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
D 【解析】∵比例系数k=?2<0,∴其图象位于二、四象限, ∵x>0,∴反比例函数的图象位于第四象限, 故选:D.查看答案和解析>>
科目:初中数学 来源:江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型:解答题
如图是由一些棱长都为1cm的小正方体组合成的简单几何体.
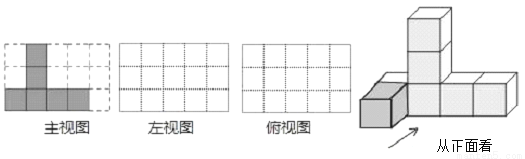
(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;
(2)如果在这个几何体上再添加一些小正方体,并保持俯视图和左视图不变,最多可以再添加________块小正方体.
6 【解析】试题分析:(1)、根据长对正,高平齐和宽相等的法则画出三视图;(2)、根据三视图的法则得出立体图形,从而得出答案. 试题解析:【解析】 (1)如图所示: ; (2)保持俯视图和左视图不变,最多可以再添加6块小正方体.查看答案和解析>>
科目:初中数学 来源:江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型:单选题
当x=3时,代数式px3+qx+1的值为2002,则当x=-3时,代数式px3+qx+1的值为( )
A. 2000 B. -2002 C. -2000 D. 2001
C 【解析】试题分析:将x=3代入代数式可得:27p+3q+1=2002,则27p+3q=2001;当x=-3时,原式=-27p-3q+1=-2001+1=-2000,故选C.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.在图3中,将三棱柱沿过点A的侧棱剪开,得到如图4的侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究.
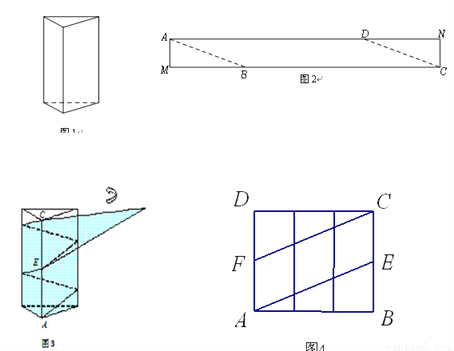
(1)请在图4中画出拼接后符合条件的平行四边形;
(2)请在图2中,计算裁剪的角度(即∠ABM的度数).
【答案】(1)作图见解析;(2)∠ABM=30°.
【解析】分析:(1)将图4中的△ABE向左平移30cm,△CDF向右平移30cm,拼成如图中的平行四边形,此平行四边形即为图2中的四边形ABCD.
(2)根据题意先求得AB=30cm,由纸带的宽为15cm,根据三角函数求得∠AMB=30°.
本题解析:(1)如图:
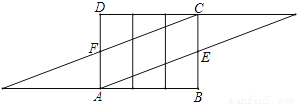
(2)由图2的包贴方法知:AB的长等于三棱柱的底边周长,∴AB=30.
∵ 纸带宽为15,∴ sin∠ABM =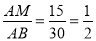 .∴∠AMB=30°.
.∴∠AMB=30°.
【题型】解答题
【结束】
11
如图,在△ABC中,∠C=45°,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.
(1)求证: 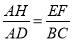 ;
;
(2)设EF=x,当x为何值时,矩形EFPQ的面积最大?并求其最大值;
(3)当矩形EFPQ的面积最大时,该矩形EFPQ以每秒1个单位的速度沿射线QC匀速运动(当点Q与点C重合时停止运动),设运动时间为t秒,矩形EFFQ与△ABC重叠部分的面积为S,求S与t的函数关系式.
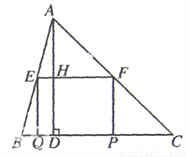
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com