练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在△ABC中，AB=7，BC=24，AC=25，则△ABC的面积是________ ．

    84． 【解析】试题分析：首先利用勾股定理逆定理判定三角形是直角三角形，然后再利用三角形的面积公式计算出面积即可． 【解析】 ∵72+242=252， ∴该三角形是直角三角形， ∴△ABC的面积是：×24×7=84， 故答案为：84．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：重庆市校2018届九年级上学期期末模拟数学试卷 题型：单选题

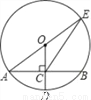
    如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB=8，CD=2，则EC的长为（ ）

    A. 2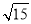 B. 8 C. 2 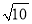D. 2

    C 【解析】连结BE，设⊙O的半径为R，由OD⊥AB，根据垂径定理得AC=BC=AB=4，在Rt△AOC中，OA=R，OC=R-CD=R-2，根据勾股定理得到（R-2）2+42=R2，解得R=5，则OC=3，由于OC为△ABE的中位线，则BE=2OC=6，再根据圆周角定理得到∠ABE=90°，然后在Rt△BCE中利用勾股定理可计算出CE． 【解析】 连结BE，设⊙O的半径为R，如图所...

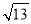
    查看答案和解析>>

    科目：初中数学 来源：江苏省东台市2017-2018学年上学期期末考试九年级数学试卷 题型：解答题

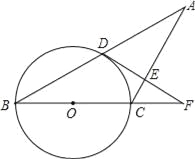
    已知：如图，△ABC中，AC=BC，以BC为直径的⊙O交AB于点D，过点D作DE⊥AC于点E，交BC的延长线于点F．

    求证：

    （1）AD=BD；

    （2）DF是⊙O的切线．

    （1）证法一：连结CD， ∵BC为⊙O的直径 ∴CD⊥AB ∵AC＝BC ∴AD＝BD． 证法二：连结CD， ∵BC为⊙O的直径 ∴∠ADC＝∠BDC＝90° ∵AC＝BC，CD＝CD ∴△ACD≌△BCD ∴AD＝BD （2）证法一：连结OD， ∵AD＝BD，OB＝OC ∴OD∥AC ∵DE⊥AC ∴DF⊥...

    查看答案和解析>>

    科目：初中数学 来源：江苏省东台市2017-2018学年上学期期末考试九年级数学试卷 题型：单选题

    有15位同学参加智力竞赛,已知他们的得分互不相同,取8位同学进入决赛,小明同学知道了自己的分数后,想知道自己能否进入决赛,还需知道这15位同学的分数的( )

    A. 平均数 B. 众数 C. 中位数 D. 最高分数

    C 【解析】【解析】 由于15个人中，第8名的成绩是中位数，故小方同学知道了自己的分数后，想知道自己能否进入决赛，还需知道这十五位同学的分数的中位数．故选C．

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：解答题

    求分式的值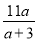： ，其中a=3．

    5.5． 【解析】试题分析：直接将a=3的值代入进行计算即可求出答案． 试题解析：把a=3代入得：原式==5.5.

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：填空题

    已知x是实数且满足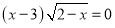，则相应的代数式x2+2x﹣1的值为________ ．

    7． 【解析】∵x是实数且满足（x﹣3）=0， ∴x﹣3=0或=0，解得x=3或x=2， ∵当x=3时，2﹣3=﹣1＜0，此时无意义， ∴x=2， 当x=2时，原式=4+4﹣1=7， 故答案为：7．

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：单选题

    如图，点O（0，0），B（0，1）是正方形OBB1C的两个顶点，以它的对角线OB1为一边作正方形OB1B2C1 ，以正方形OB1B2C1的对角线OB2为一边作正方形OB2B3C2 ，再以正方形OB2B3C2的对角线OB3为一边作正方形OB3B4C3 ，…，依次进行下去，则点B6的坐标是（　　）

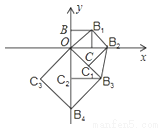
    A. （﹣8，0） B. （0，﹣8） C. 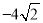（，0） D. 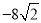（，0）

    A 【解析】如图所示 ∵四边形OBB1C是正方形， ∴OB1=，B1所在的象限为1； ∴OB2=（）2， B2在x轴正半轴； ∴OB3=（）3，B3所在的象限为第四象限； ∴OB4=（）4，B4在y轴负半轴； ∴OB6=（）6=8，B6在x轴负半轴， ∴B6（﹣8，0）， 故选A．

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：填空题

    分式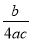与的最简公分母是________．

    12a2bc． 【解析】【解析】 找出各个因式的最高次幂，乘积就是分母的最简公分母．分式与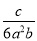的最简公分母是12a2bc．故答案为：12a2bc．

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2017-2018学年八年级上学期期末模拟数学试卷 题型：单选题

    如图，∠A=15°，AB=BC=CD=DE=EF，则∠DEF等于（ ）

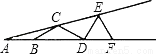
    A．90° B．75° C．70° D．60°

    D 【解析】 试题分析:根据已知条件，利用等腰三角形的性质及三角形的内角和外角之间的关系进行计算． 【解析】 ∵AB=BC=CD=DE=EF，∠A=15°， ∴∠BCA=∠A=15°， ∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°， ∴∠BCD=180°﹣（∠CBD+∠BDC）=180°﹣60°=120°， ∴∠ECD=∠CED=180°...

    查看答案和解析>>

    同步练习册答案