练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    多项式2b+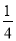ab2﹣5ab﹣1的次数为_____．

    3 【解析】多项式的次数就是多项式中最高次项的次数． 【解析】 根据题意得：多项式2b+ab2﹣5ab﹣1次数为3． 故答案为：3．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省德州市2018届九年级上期中数学试卷 题型：单选题

    如图，⊙O的半径为5，弦AB的长为8，点M在线段AB（包括端点A，B）上移动，则OM的取值范围是（　　）

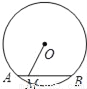
    A. 3≤OM≤5 B. 3≤OM＜5 C. 4≤OM≤5 D. 4≤OM＜5

    A 【解析】试题分析：当M与A或B重合时，达到最大值；当OM⊥AB时，为最小． 【解析】 当M与A或B重合时，达到最大值，即圆的半径5； 当OM⊥AB时，为最小值==3． 故OM的取值范围是：3≤OM≤5． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：江苏省丹阳市2017-2018学年七年级12月月考数学试卷 题型：解答题

    解方程：

    （1）2（2x﹣3）﹣3 = 2﹣3（x﹣1）

    （2）

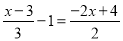
    （1）x=2（2）x=3 【解析】按解一元一次方程一般步骤解方程即可. 【解析】 （1）去括号，得4x-6-3=2-3x+3, 移项，得4x+3x=2+3+6+3, 合并同类项得，7x=14, 系数化为1得，x=2； （2）去分母得，2(x-3)-6=3(-2x+4), 去括号，得2x-6-6=-6x+12, 移项，得2x+6x=12+6+6, ...

    查看答案和解析>>

    科目：初中数学 来源：江苏省丹阳市2017-2018学年七年级12月月考数学试卷 题型：填空题

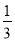    x2y是__次单项式．

    3 【解析】根据单项式次数的概念可知x2y是3次单项式， 故答案为：3.

    查看答案和解析>>

    科目：初中数学 来源：广西贵港市港南区2017-2018学年七年级（上）期中数学试卷 题型：解答题

    已知a+b=0，且a，b均不等于零，c，d互为倒数，且|x|=0.3，求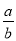： +c•d+x2的值．

    0.09. 【解析】根据相反数、倒数以及绝对值进行计算即可． 【解析】 ∵a+b=0，且a，b均不等于零，c，d互为倒数，且|x|=0.3， ∴a=﹣b，cd=1，x=±0.3， ∴原式=﹣1+1+0.09=0.09．

    查看答案和解析>>

    科目：初中数学 来源：广西贵港市港南区2017-2018学年七年级（上）期中数学试卷 题型：单选题

    下面说法正确的有（　　）

    ①π的相反数是﹣3.14；②符号相反的数互为相反数；③﹣（﹣3.8）的相反数是3.8；④一个数和它的相反数不可能相等；⑤正数与负数互为相反数．

    A. 0个 B. 1个 C. 2个 D. 3个

    A 【解析】试题分析：①π的相反数是－π，故 ①错误；②符号相反的数不一定是相反数，故②错误；③-（-3．8）=3．8，所以 -（-3．8）的相反数是-3．8，故③错误；④ 0的相反数是0，所以一个数和它的相反数不可能相等是错误的，故④错误；⑤正数与负数不一定是相反数，所以正数与负数互为相反数是错误的，故⑤错误．所以正确的个数有0个． 故选：A．

    查看答案和解析>>

    科目：初中数学 来源：广西贵港市港南区2017-2018学年七年级（上）期中数学试卷 题型：单选题

    代数式﹣x3+2x+24是（　　）

    A. 多项式 B. 三次多项式 C. 三次三项式 D. 四次三项式

    C 【解析】多项式中的每个单项式叫做多项式的项，有几个单项式即是几项式，由此判定﹣x3+2x+24有三项，是三项式；一个多项式里次数最高项的次数，叫做这个多项式的次数，由于﹣x3是最高次项，由此得出﹣x3+2x+24的次数是3． 【解析】 代数式﹣x3+2x+24是﹣x3、2x、24这三项的和，其中﹣x3是最高次项， ∴﹣x3+2x+24是三次三项式． 故选C． ...

    查看答案和解析>>

    科目：初中数学 来源：吉林省松原市2018届九年级上期末模拟数学试卷 题型：填空题

    已知实数m是关于x的方程x2-3x-1=0的一根，则代数式2m2-6m+2值为________．

    4 【解析】试题分析：把x=m代入方程得出m2﹣3m﹣1=0，求出m2﹣3m=1，推出2m2﹣6m=2，把上式代入2m2﹣6m+2，得到2m2﹣6m+2=2+2=4， 故答案为：4．

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：解答题

    如图，AD平分∠BAC，∠ABD+∠ACD=180°，∠ABD＜90°，求证：DB=DC．

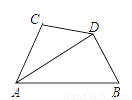
    证明见解析． 【解析】试题分析：在AB上截取AE=AC，连接DE，可证明△ACD≌△AED，可得CD=DE，再由条件可证明∠ABD=∠DEB，可证得DB=DC． 试题解析：在AB上截取AE=AC，连接DE， ∵AD平分∠BAC， ∴∠CAD=∠EAD， 在△ACD和△AED中， AE=AC，∠CAD=∠EAD，AD=AD， ∴△ACD≌△AED（SAS），...

    查看答案和解析>>

    同步练习册答案