
直线y=3x+2沿y轴向下平移4个单位,则平移后直线与y轴的交点坐标为_______.
(0,-2) 【解析】y=3x+2沿y轴向下平移4个单位y=3x+2-4=3x-2, 令x=0,y=-2, 所以(0,-2). 故交点坐标(0,-2).科目:初中数学 来源:2017年广西防城港市中考数学模拟试卷 题型:单选题
如图所示,已知DE∥BC,CD是∠ACB的平分线,∠B=72°,∠ACB=40°,那么∠BDC等于( )
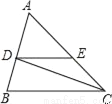
A. 78° B. 90° C. 88° D. 92°
C 【解析】分析:先根据CD是∠ACB的平分线,∠ACB=40°,求出∠BCD的度数,再由三角形内角和定理便可求出∠BDC的度数. 解答:【解析】 ∵CD是∠ACB的平分线,∠B=72°,∠ACB=40°,∴∠BCD=20°, 在△BCD中,∠B=72°,∠BCD=20°,∴∠BDC=180°-72°-20°=88°. 故选C.查看答案和解析>>
科目:初中数学 来源:山东省诸城市2017-2018学年七年级上学期第二次月考数学试卷 题型:填空题
用代数式表示“a的相反数与b的倒数的和的平方”:_________________________.
(﹣a+)2 【解析】试题解析:∵a的相反数与b的倒数的和为 ∴a的相反数与b的倒数的和的平方为 故答案为:查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017-2018学年八年级12月联合质量调研数学试卷 题型:解答题
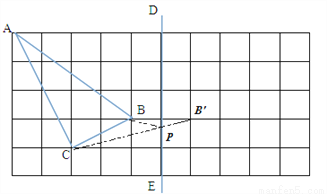
如图,在所给正方形网格(每个小网格的边长是1)图中完成下列各题.
(1)格点△ABC(顶点均在格点上)的面积=_________;
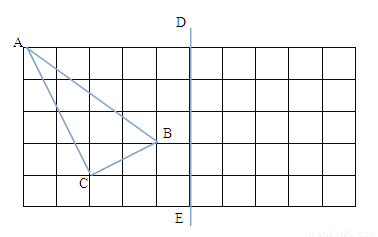
(2)画出格点△ABC关于直线DE对称的△A1B1C1;
(3)在DE上画出点P,使PB+PC最小,并求出这个最小值.
【答案】(1)面积等于5(2)图形见解析(3)最小值是根号17
【解析】试题分析:(1)利用勾股定理求出三角形边长,并证明是直角三角形求面积.(2)画出A,B,C的对称点A1,B2,C3,连接三角形.(3)利用对称利用两点之间直线最短求最小值.
试题解析:
(1)分别利用勾股定理求得AC=2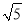 ,AB=
,AB=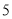 ,BC=
,BC=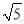 ,
, 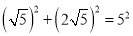 ,所以∠ACB=90°,面积等于
,所以∠ACB=90°,面积等于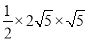 =5.
=5.
(2)画出A,B,C的对称点A1,B2,C3,连接三角形.如下图.
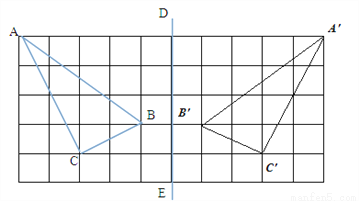
(3)作B点对称B’,连接B’C交DE于P,B’P+PC=BP+CP,所以使PB+PC最小.
利用勾股定理B’C=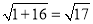 ,
,
所以最小值是根号17.
点睛:平面上最短路径问题
(1)归于“两点之间的连线中,线段最短”.凡属于求“变动的两线段之和的最小值”时,大都应用这一模型.
(2)归于“三角形两边之差小于第三边”.凡属于求“变动的两线段之差的最大值”时,大都应用这一模型.
(3)平面图形中,直线同侧两点到直线上一点距离之和最短问题.
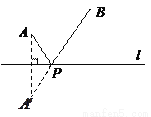
【题型】解答题
【结束】
23
已知一次函数y=kx+7的图像经过点A(2,3).
(1)求k的值;
(2)判断点B(-1,8),C(3,1)是否在这个函数的图像上,并说明理由;
(3)当-3<x<-1时,求y的取值范围.
(1)k=-2(2)点B不在,点C在,(3)9<y<13 【解析】 试题分析:(1)把点A(2,3)代入y=kx+7即可求出k的值;(2)点B(-1,8),C(3,1)的横坐标代入函数解析式验证即可;(3)根据x的取值范围,即可求出y的取值范围. 试题解析:(1)把点A(2,3)代入y=kx+7得:k=-2 (2)当x=-1时,y=-2×(-1)+7=9 ∵9≠8∴点...查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017-2018学年八年级12月联合质量调研数学试卷 题型:填空题
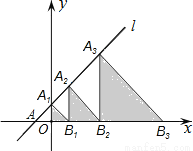
如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,…在直线l上,点B1,B2,B3,…在x轴的正半轴上,若△A1OB1,△A2B1B2,△A3B2B3,…,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形AnBn﹣1Bn顶点Bn的横坐标为________________.
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017-2018学年八年级12月联合质量调研数学试卷 题型:单选题
已知A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A.两人同时出发,各自到达终点后停止.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下图中正确反映s与t之间函数关系的是( )
A. 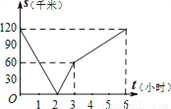 B.
B. 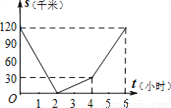
C. 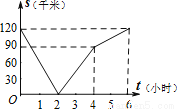 D.
D. 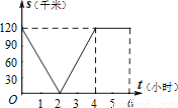
查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西师大附中七年级(下)第一次月考数学试卷 题型:解答题
两个大小不同的等腰直角三角形三角板按图1所示的位置放置,图2是由它抽象出的几何图形,AB=AC,AE=AD,∠BAC=∠EAD=90°,B,C,E在同一条直线上,连接DC.
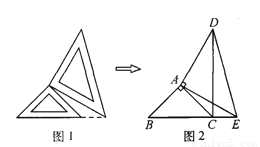
(1)请找出图2中与△ABE全等的三角形,并给予证明;
(2)证明:DC⊥BE.
(1)△ACD≌△ABE.证明见解析;(2)证明见解析. 【解析】 试题分析:根据等腰直角三角形的性质利用SAS判定△ABE≌△ACD;因为全等三角形的对应角相等,所以∠ACD=∠ABE=45°,已知∠ACB=45°,所以可得到∠BCD=∠ACB+∠ACD=90°,即DC⊥BE. 试题解析:(1)【解析】 图2中△ACD≌△ABE. 证明:∵△ABC与△AED均为等腰直角...查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西师大附中七年级(下)第一次月考数学试卷 题型:单选题
已知△ABC的边长分别为a,b,c,化简|a+b﹣c|﹣|b﹣a﹣c|的结果是( )
A. 2a B. ﹣2b C. 2a+3b D. 2b﹣2c
D 【解析】 试题分析:要求它们的值,就要知道它们的绝对值里的数是正数还是负数,根据三角形三边关系:两边之和大于第三边,两边之差小于第三边可知. 【解析】 a+b﹣c>0,b﹣a﹣c<0. 所以|a+b﹣c|﹣|b﹣a﹣c| =a+b﹣c﹣[﹣(b﹣a﹣c)] =2b﹣2c. 故选D.查看答案和解析>>
科目:初中数学 来源:重庆市江津区2016-2017学年八年级下学期期末考试数学试卷 题型:解答题
如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,过O点作EF∥BC,交AB于E,交AC于F.
(1)判断△BEO的形状,并说明理由.
(2)若AB=5cm,AC=4cm,求△AEF的周长.
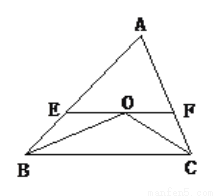
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com