
科目:初中数学 来源:江苏省东部分校2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
已知方程 的解也满足方程
的解也满足方程 .
.
(1)求m、n的值;
(2)已知线段AB=m,在直线AB上取一点C,恰好使AC=n,点Q为AB的中点,求线段CQ的长.
(1)m=6,n=2;(2)CQ=1或5 【解析】试题分析:(1)解方程3m-4=2(m+1),得到m的值,再代入方程2(6-3)=n+4,得到n的值; (2)由中点定义得到AQ=BQ=3,然后分两种情况讨论即可. 试题解析:(1)解方程3m-4=2(m+1)得:m=6,∴2(6-3)=n+4,解得:n=2; (2)∵AM=6,点Q为AB的中点,∴AQ=BQ=3,∵AC=2...查看答案和解析>>
科目:初中数学 来源:浙江杭州富阳2016-2017学年八年级上学期期末数学试卷 题型:单选题
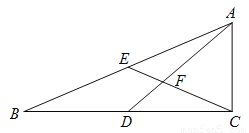
如图所示,在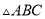 中,
中, 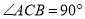 ,点
,点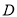 在
在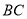 上,
上, 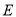 是
是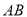 的中点,
的中点, 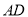 与
与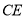 交于点
交于点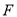 ,且
,且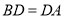 ,若
,若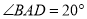 ,则
,则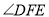 等于( )
等于( )
A. 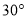 B.
B. 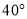 C.
C. 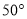 D.
D. 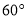
查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
△ABC是等腰三角形,腰上的高为8cm,面积为40cm2,则该三角形的周长是_______cm.
或. 【解析】(1)如图1,在△ABC中,AB=AC,∠A是锐角,BD是AC边上的高, 由题意可知:BD=8cm,S△ABC=BD·AC=40cm2, ∴AC=10cm=BC, ∴在Rt△ABD中,由勾股定理可得:AD=(cm), ∴DC=AC-AD=4cm, ∴在Rt△BDC中,由勾股定理可得:BC=(cm), ∴此时△ABC的周长=AB+AC+BC=(...查看答案和解析>>
科目:初中数学 来源:北师大版八年级数学上册 第七章 平行线的证明 单元测试 题型:解答题
已知:如图,E、F是平行四边行ABCD的对角线AC上的 两点,AE=CF。
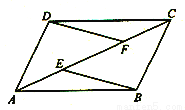
求证:(1)△ADF≌△CBE
(2)EB∥DF.
∵四边形ABCD为平行四边形, ∴AD∥BC,AD=BC. ………………(1分) ∴∠DAC=∠BCE. 又∵AE=CF,∴AF=CE ∴△ADF≌△CBE.……………………(4分) ∴∠AFD=∠CEB. ∴BE∥DF. ……………………………(6分 【解析】试题分析:要证△ADF≌△CBE,因为AE=CF,则两边同时加上EF,得到AF=CE,又因为AB...查看答案和解析>>
科目:初中数学 来源:北师大版八年级数学上册 第七章 平行线的证明 单元测试 题型:填空题
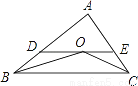
已知,如图,在△ABC中,BO和CO分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为________.
查看答案和解析>>
科目:初中数学 来源:四川省宜宾市2017-2018学年上学期期末教学质量监测八年级数学试卷 题型:解答题
任意一个正整数都可以进行这样的分【解析】
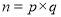 (
(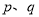 是正整数,且
是正整数,且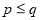 ),正整数的所有这种分解中,如果
),正整数的所有这种分解中,如果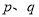 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称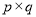 是正整数的最佳分解.并规定:
是正整数的最佳分解.并规定: 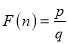 .例如24可以分解成1×24,2×12,3×8或4×6,因为
.例如24可以分解成1×24,2×12,3×8或4×6,因为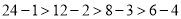 ,所以4×6是24的最佳分解,所以
,所以4×6是24的最佳分解,所以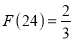 .
.
(1)求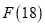 的值;
的值;
(2)如果一个两位正整数, 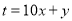 (
(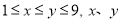 为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差记为
为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差记为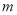 ,交换其个位上的数与十位上的数得到的新数加上原来的两位正整数所得的和记为
,交换其个位上的数与十位上的数得到的新数加上原来的两位正整数所得的和记为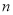 ,若
,若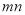 为4752,那么我们称这个数为“最美数”,求所有“最美数”;
为4752,那么我们称这个数为“最美数”,求所有“最美数”;
(3)在(2)所得“最美数”中,求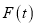 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源:北师大版数学九年级上册第二章第三节《用公式法求解一元一次方程》课时练习 题型:单选题
用公式法解方程6x-8=5x2时,a、b、c的值分别是( )
A. 5、6、-8 B. 5、-6、-8 C. 5、-6、8 D. 6、5、-8
C 【解析】【解析】 原方程可化为5x2-6x+8=0,∴a=5,b=-6,c=8.故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com