
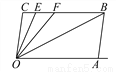
��ͼ����֪����CB��OA����C����OAB��100�㣬��E��F��CB�ϣ��������FOB����AOB��OEƽ�֡�COF.
(1)���EOB�Ķ�����
(2)������ƽ��AB���������������䣬��ô��OBC�á�OFC��ֵ�Ƿ���֮�仯�����仯���ҳ��仯���ɣ������䣬��������ֵ��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���Ĵ�ʡ������2018����꼶��ѧ�ڽ�ѧˮƽ�����ѧ�Ծ� ���ͣ���ѡ��
���κ���y=-x2+6-7����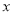 ȡֵΪt��x��t+2ʱ�������ֵy���ֵ=-��t-3��2+2����
ȡֵΪt��x��t+2ʱ�������ֵy���ֵ=-��t-3��2+2����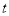 ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ
A. t��0 B. 0��t��3 C. t��3 D. ���϶�����
C �������������������y=-x2+6x-7=-��x-3��2+2�� ��t��3��t+2ʱ����1��t��3ʱ������Ϊ�������� ymax=f��3��=2����ymax=-��t-3��2+2ì�ܣ� ��3��t+2ʱ����t��1ʱ��ymax=f��t+2��=-��t-1��2+2����ymax=-��t-3��2+2ì�ܣ� ��3��t����t��3ʱ��ymax=f��t��=-��t-3��2+2��������ȣ� ��t��ȡֵ��Χt��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������У2017-2018ѧ�����꼶��ѧ�ڵڶ��ο�����ѧ�Ծ� ���ͣ���ѡ��
���������У���ȷ����( )
A. 3m+2n=5mn B. 4a2+3a3=7a5 C. 5a2b-3ba2=2a2b D. 5a2-4a2=1
C ��������A. 3m��2n����ͬ������ܺϲ����ʴ���B. 4a2��3a3����ͬ������ܺϲ����ʴ���C. 5a2b-3ba2=2a2b ����ȷ��D. 5a2-4a2=a2���ʴ��� ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018����ѧ��ʦ�����꼶��ѧ�²����в����Ծ� ���ͣ������
(cos 30��+sin 45��)(sin 60��-cos 45��)=____.
�����������������ԭʽ �ʴ�Ϊ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018����ѧ��ʦ�����꼶��ѧ�²����в����Ծ� ���ͣ���ѡ��
��ͼ��ʾ���ڡ�ABC�У� cos B��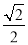 ��sin C��
��sin C��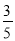 ��BC��7�����ABC�������(����)
��BC��7�����ABC�������(����)
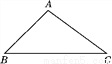
A. 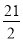 B. 12 C. 14 D. 21
B. 12 C. 14 D. 21
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ�²ᣨ�˽̰棩��ĩ����� ���ͣ������
��ƽ��ֱ������ϵ�У���ABC�ı�AB��x���ϣ���AB��3������A������Ϊ(2��0)������C������Ϊ(��2��5)��
(1)�������з��������ġ�ABC����д����B�����ꣻ
(2)���ABC�������
(1) (��1��0)��(5��0)(2) �������������������1������ƽ��ֱ������ϵ���ֵ��ڵ����ߺ��ұ��������д����B�����꼴�ɣ� ��2�����������ε������ʽ��ʽ���㼴�ɵý⣮ ��������� (1)��ͼ��ʾ�� ��Ϊ��������Ϊ�� (2)�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ�²ᣨ�˽̰棩��ĩ����� ���ͣ������
ѧϰίԱ���鱾��ѧ�������Ķ��������ѧ��ϲ�����鼮���з���ͳ�ƣ����С���ʫ���ࡱ��Ƶ��Ϊ12�ˣ�Ƶ��Ϊ0.25����ô�������ѧ������Ϊ______��
48�� ������������������豻�����ѧ������Ϊx�ˣ� ����=0.25�� ���x=48�� ������x=48�Ƿ��̵Ľ⣮ �ʴ�Ϊ48���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�人�к�ɽ��2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��֪������y=x2��2mx+m2��1��m�dz������Ķ���ΪP��ֱ��l��y=x��1��
��1����֤����P��ֱ��l�ϣ�
��2���������ߵĶԳ���Ϊx=��3��ֱ��д���������ߵĶ��������� ������x�ύ������Ϊ�� ����
��3���ڣ�2�������£��������ϵ㣨��2��b����ͼ���ϵĶԳƵ���������� ����
����4����3�� �������������������1�������䷽���õ�y=��x��m��2+m��1����P��m��m��1����Ȼ�����һ�κ���ͼ���ϵ�����������жϵ�P��ֱ��l�ϣ� ��2���ɣ�1����֪�����ߵĶԳ���Ϊx=m�������֪������ɵ�m=��3����������������ߵĶ������ꣻ��y=0����x�ύ������Ҳ������� ��3���ѵ㣨��2��b�����������߽���ʽ�����b��ֵ�������������ͼ���ϵĶԳƵ�����꣮ ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡƽ���������2017-2018ѧ��ȵ�һѧ����ĩ��ѧ�Ծ����� ���ͣ���ѡ��
��֪x2-2x=8����3x2-6x-18��ֵΪ��������
A. 54 B. 6 C. -10 D. -18
B ���������������� 3x2-6x-18=3��x2-2x��-18=3��8-18=6����ѡB���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com