练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

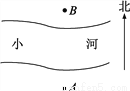
    如图所示的A、B是两根呈南北方向排列的电线杆，A、B之间有一条小河，小刚想估测这两根电线杆之间的距离，于是小刚从A点开始向正西方向走了20步到达一棵大树C处，接着又向前走了20步到达D处，然后他左转90°直行，当他看到电线杆B、大树C和他自己现在所处的位置E恰在同一条直线上时，他从D位置走到E处恰好走了100步，利用上述数据，小刚测出了A、B两根电线杆之间的距离．

    (1)请你根据上述的测量方法在原图上画出示意图；

    (2)如果小刚一步大约60厘米，请你求A、B两根电线杆之间的距离并简述理由．

    (1)图略 (2)AB＝60m 【解析】分析：（1）认真读题，根据题意画出示意图；（2）结合题意分别求出AC、DC、DE的长，易得：AC=DC，∠BAC=∠EDC，∠DCE=∠ACB，根据全等三角形的判定定理可得△ABC≌△DEC，进而得到AB=DE，据此，可得出结果. 本题解析：（1）根据题意画出图形，如图所示. （2）A、B两根电线杆之间的距离大约为36m.理由如下. ...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版数学七年级下册第三章3.1用表格表示的变量间关系课时练习 题型：单选题

    当前，雾霾严重，治理雾霾方法之一是将已生产的PM2.5吸纳降解，研究表明：雾霾的程度随城市中心区立体绿化面积的增大而减小，在这个问题中，自变量是（ ）

    A.雾霾程度 B.PM2.5

    C.雾霾 D.城市中心区立体绿化面积

    D 【解析】 试题分析：根据函数的关系，可得答案． 解；雾霾的程度随城市中心区立体绿化面积的增大而减小， 雾霾的程度是城市中心区立体绿化面积的函数，城市中心区立体绿化面积是自变量， 故选：D．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型：单选题

    若一个三角形的两边长分别为3和7，则第三边长可能是（ ）

    A．6 B．3 C．2 D．11

    A. 【解析】 试题分析：根据三角形三边关系，两边之和第三边，两边之差小于第三边可得4＜第三边长＜10，所以符合条件的整数为6，故答案选A．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型：填空题

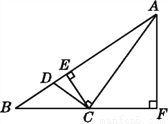
    如图,在△ABC中,BC边上的高是____;在△BCE中,BE边上的高是____;在△ACD中,AC边上的高是____.

    AF CE CD 【解析】【解析】 在△ABC中，BC边上的高是AF；在△BCE中，BE边上的高是CE；在△ACD中，AC边上的高是CD．故答案为：AF，CE，CD．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型：填空题

    已知三角形的三条中线交于一点,则下列结论:①这一点在三角形的内部;②这一点有可能在三角形的外部;③这一点是三角形的重心.其中正确的结论有____.(填序号)

    ①③ 【解析】【解析】 三角形的三条中线的交点一定在三角形内部，这个交点叫三角形的重心．故①③正确．故答案为：①③．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型：单选题

    把等腰直角三角形的三角板按如图所示的方式立在桌面上，顶点A顶着桌面，若另两个顶点分别距离桌面5cm和3cm，则过另外两个顶点向桌面作垂线，则垂足之间的距离即DE的长为( )

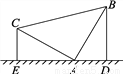
    A. 4cm B. 6cm C. 8cm D. 求不出来

    C 【解析】∵ ∠BAC=90° ∠AEC=90° ∴ ∠BAC=∠AEC ∵ ∠DAB+∠BAC=∠DAC ∠ECA+∠AEC=∠DAC ∠BAC=∠DEC ∴ ∠ECA=∠DAB ∵ △ABD是直角三角形 △CAE是直角三角形 AB=AC ∠ECA=∠DAB ∴ △ABD≌△CAE (一边一锐角对应相等的两个直角三角形全等) ∴ AE=BD AD=CE...

    查看答案和解析>>

    科目：初中数学 来源：内蒙古包头市青山区2017-2018学年八年级（上）期末数学试卷 题型：解答题

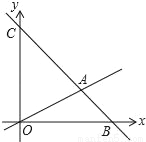
    如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2），动点M在线段OA和射线AC上运动．

    （1）求直线AB的解析式．

    （2）求△OAC的面积．

    （3）是否存在点M，使△OMC的面积是△OAC的面积的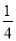？若存在求出此时点M的坐标；若不存在，说明理由．

    （1）y=﹣x+6；（2）12；（3）M1（1， ）或M2（1，5）或M3（﹣1，7）． 【解析】试题分析：（1）利用待定系数法即可求得函数的解析式； （2）求得C的坐标，即OC的长，利用三角形的面积公式即可求解； （3）当△OMC的面积是△OAC的面积的时，根据面积公式即可求得M的横坐标，然后代入解析式即可求得M的坐标． 【解析】 （1）设直线AB的解析式是y=kx+b...

    查看答案和解析>>

    科目：初中数学 来源：内蒙古包头市青山区2017-2018学年八年级（上）期末数学试卷 题型：单选题

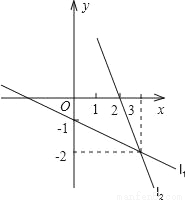
    如图中的两直线l1、l2的交点坐标可以看作哪个方程组的解（　　）

    A. B. C. D.

    A 【解析】试题解析：由于直线l1经过点（0，﹣1），（3，﹣2）；因此直线l1的解析式为y=﹣x﹣1； 同理可求得直线l2的解析式为y=﹣2x+4； 因此直线l1，l2的交点坐标可以看作方程组的解． 故选A．

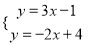
    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下5.3.1 等腰三角形的性质 同步练习 题型：单选题

    如图,四边形ABCD是正方形,△PAD是等边三角形,则∠BPC等于(　　)

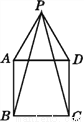
    A. 20° B. 30° C. 35° D. 40°

    B 【解析】试题解析：∵四边形ABCD是正方形，△PAD是等边三角形， ∵PA=AD，AB=AD， ∴PA=AB， 同理： ， 故选B.

    查看答案和解析>>

    同步练习册答案