
如图所示,△ABC为等边三角形,P为BC上一点,Q为AC上一点,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则对下面四个结论判断正确的是( )
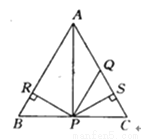
①点P在∠BAC的平分线上, ②AS=AR, ③QP∥AR, ④△BRP≌△QSP.
A. 全部正确; B. 仅①和②正确; C. 仅②③正确; D. 仅①和③正确
A 【解析】试题解析:∵PR⊥AB于R,PS⊥AC于S. ∴∠ARP=∠ASP=90°. ∵PR=PS,AP=AP. ∴Rt△ARP≌Rt△ASP. ∴AR=AS,故(2)正确,∠BAP=∠CAP. ∴AP是等边三角形的顶角的平分线,故(1)正确. ∴AP是BC边上的高和中线,即点P是BC的中点. ∵AQ=PQ. ∴点Q是AC的中点. ∴...科目:初中数学 来源:四川省遂宁市黄泥学校2016-2017学年上期八年级期中测评数学试卷 题型:解答题
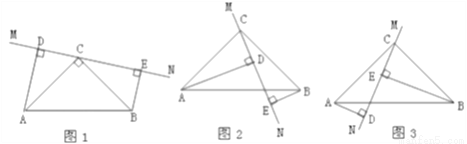
在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系.
查看答案和解析>>
科目:初中数学 来源:重庆市江津区2016-2017学年八年级下学期期末考试数学试卷 题型:填空题
如图,∠ABC=∠DCB,请补充一个条件: ,使△ABC≌△DCB.
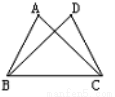
查看答案和解析>>
科目:初中数学 来源:重庆市江津区2017-2018学年八年级上学期第二次六校联考数学试卷 题型:解答题
近年来,由于受国际石油市场的影响,汽油价格不断上涨.下面是小明与爸爸的对话:
小明:“爸爸,听说今年5月份的汽油价格上涨了不少啊!”
爸爸:“是啊,今年5月份每升汽油的价格是去年5月份每升汽油的价格的 倍,用150元给汽车加的油量比去年少11.25升.”
倍,用150元给汽车加的油量比去年少11.25升.”
小明:“今年5月份每升汽油的价格是多少呢?”
聪明的你,根据上面的对话帮小明计算一下今年5月份每升汽油的价格?
今年5月份每升汽油的价格是8元. 【解析】试题分析:设去年5月份的石油价格为每升x元,则今年5月份的石油价格为每升1.6x元,根据用150元给汽车加的油量比去年少11.25升,列出方程求解即可. 试题解析:设去年5月份每升汽油的价格是x元,则今年5月份每升汽油的价格是1.6x元. 根据题意得: 解得x=5. 经检验:x=5是原方程的解, ∴(元); 答:...查看答案和解析>>
科目:初中数学 来源:重庆市江津区2017-2018学年八年级上学期第二次六校联考数学试卷 题型:填空题
如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若△ADE的周长为20cm,则BC= cm.
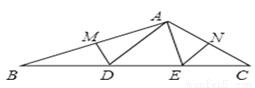
查看答案和解析>>
科目:初中数学 来源:重庆市江津区2017-2018学年八年级上学期第二次六校联考数学试卷 题型:单选题
一艘轮船在静水中的最大航速为30千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少?设江水的流速为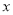 千米/时,则可列方程( )
千米/时,则可列方程( )
A. 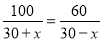 B.
B. 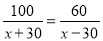
C. 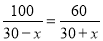 D.
D. 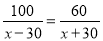
查看答案和解析>>
科目:初中数学 来源:2017年广东省河源市中考数学一诊试卷 题型:解答题
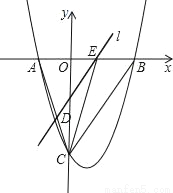
如图,抛物线y=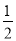 x2﹣
x2﹣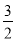 x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源:2017年广东省河源市中考数学一诊试卷 题型:单选题
在平面直角坐标系中,点P(-2,-3)所在的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
C 【解析】试题解析:点P(-2,-3)的横坐标和纵坐标均为负数,所以点P(-2,-3) 在第三象限. 故选C.查看答案和解析>>
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:填空题
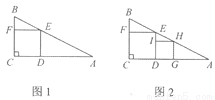
我们定义:“四个顶点都在三角形边上的正方形是三角形的内接正方形”.已知:在Rt△ABC中,∠C=90°,AC=6,BC=3.
(1)如图l,四边形CDEF是△ABC的内接正方形,则正方形CDEF的边长a1是________;
(2)如图2,四边形DGHI是(1)中△EDA的内接正方形,那么第2个正方形DGHI的边长记为a2;继续在图2中的△HGA中按上述方法作第3个内接正方形……以此类推,则第n个内接正方形的边长an=____. (n为正整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com