
如图,直线a∥b,∠1=75°,∠2=35°,则∠3的度数是( )
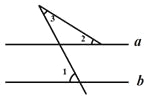
A. 75° B. 55° C. 40° D. 35°
C 【解析】试题分析:如图,根据平行线的性质可得∠1=∠4=75°,然后根据三角形的外角等于不相邻两内角的和,可知∠4=∠2+∠3,因此可求得∠3=75°-35°=40°. 故选C科目:初中数学 来源:重庆市江津区2016-2017学年八年级下学期期末考试数学试卷 题型:解答题
已知CD是经过∠BCA顶点C的一条直线,CA=CB.E、F分别是直线CD上两点,且∠BEC=∠CFA=∠ .
.
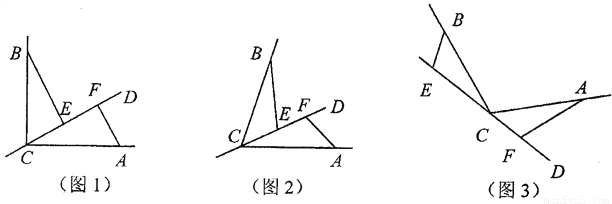
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面问题:
①如图1若∠BCA=90°,∠ =90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.
=90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.
②如图2,若0°<∠BCA<180°, 请添加一个关于∠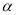 与∠BCA关系的条件___ ____使①中的结论仍然成立;
与∠BCA关系的条件___ ____使①中的结论仍然成立;
(2)如图3,若直线CD经过∠BCA的外部,∠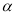 =∠BCA,请写出三条线段EF、BE、AF的数量关系并证明你的结论.
=∠BCA,请写出三条线段EF、BE、AF的数量关系并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:重庆市江津区2017-2018学年八年级上学期第二次六校联考数学试卷 题型:单选题
一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )
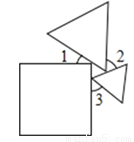
A. 90° B. 100° C. 130° D. 180°
B 【解析】试题解析:如图, ∠BAC=180°-90°-∠1=90°-∠1,. ∠ABC=180°-60°-∠3=120°-∠3,. ∠ACB=180°-60°-∠2=120°-∠2,. 在△ABC中,∠BAC+∠ABC+∠ACB=180°,. ∴90°-∠1+120°-∠3+120°-∠2=180°,. ∴∠1+∠2=150°-∠3,. ∵∠3=...查看答案和解析>>
科目:初中数学 来源:2017年广东省河源市中考数学一诊试卷 题型:解答题
先化简,再求值: 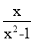 ÷(1+
÷(1+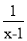 ),其中x=
),其中x=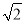 ﹣1.
﹣1.
查看答案和解析>>
科目:初中数学 来源:2017年广东省河源市中考数学一诊试卷 题型:单选题
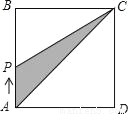
如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x之间形成的函数关系图象大致是( )
A.  B.
B. 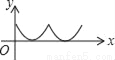 C.
C. 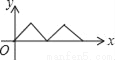 D.
D. 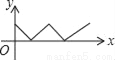
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(C卷) 题型:解答题
如图①,先把一矩形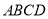 纸片上下对折,设折痕为
纸片上下对折,设折痕为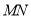 ;如图②,再把
;如图②,再把
点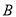 叠在折痕线
叠在折痕线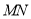 上,得到
上,得到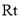
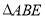 .过
.过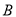 点作
点作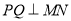 ,分别交
,分别交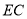 、
、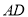 于点
于点 、
、 .
.
(1)求证: 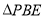 ∽
∽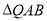 ;
;
(2)在图②中,如果沿直线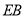 再次折叠纸片,点
再次折叠纸片,点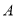 能否叠在直线
能否叠在直线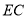 上?请说明理由;
上?请说明理由;
(3)在(2)的条件下,若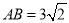 ,求
,求 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(C卷) 题型:填空题
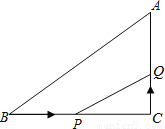
如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从点B出发,沿BC以2 cm /s的速度向点C移动,点Q从点C出发,以1cm/s的速度向点A移动,若点P、Q分别从点B、C同时出发,设运动时间为ts,当t=________时,△CPQ与△CBA相似.
查看答案和解析>>
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:解答题
问题探究:
新定义:
将一个平面图形分为面积相等的两部分的直线叫做该平面图形的“等积线”,其“等积线”被该平面图形截得的线段叫做该平面图形的“等积线段”(例如圆的直径就是圆的“等积线段”)
解决问题:
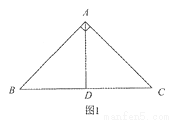
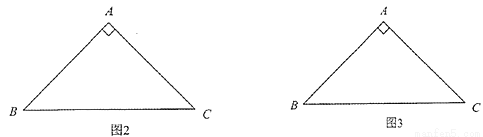
已知在Rt△ABC中,∠BAC=90°,AB=AC=2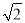 .
.
(1)如图1,若AD⊥BC,垂足为D,则AD是△ABC的一条等积线段,直接写出AD的长;
(2)在图2和图3中,分别画出一条等积线段,并直接写出它们的长度. (要求:图1、图2和图3中的等积线段的长度各不相等)
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省张掖市中考数学三模试卷 题型:单选题
抛物线y=ax2+bx+c(a≠0)的图象如图所示,则下列说法正确的是( )
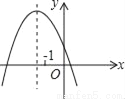
A. b2﹣4ac<0 B. abc<0 C. 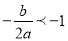 D. a﹣b+c<0
D. a﹣b+c<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com