
将函数y=x2+6x+7进行配方正确的结果应为( )
A、y=(x+3)2+2 B、y=(x-3)2+2
C、y=(x+3)2-2 D、y=(x-3)2-2
C. 【解析】 试题分析:利用配方法把一般式转化成顶点式即可. 试题解析:y=x2+6x+7=(x2+6x+9)-9+7=(x+3)2-2 故选C.科目:初中数学 来源:江西省景德镇市2017-2018学年八年级上学期期末质量检测数学试卷 题型:解答题
请认真阅读下列这道例题的解法,并完成后面两问的作答:
例:已知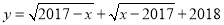 ,求
,求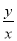 的值.
的值.
【解析】
由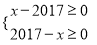 ,解得:
,解得: 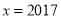 ,∴
,∴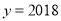 .∴
.∴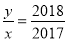 .
.
请继续完成下列两个问题:
(1)若x、y为实数,且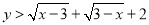 ,化简:
,化简: 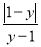 ;
;
(2)若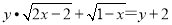 ,求
,求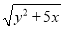 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:宁夏中卫市2018届九年级(上)期中数学试卷 题型:单选题
如图,在△ABC中,D,E是AB边上的点,且AD=DE=EB,DF∥EG∥BC,则△ABC被分成三部分,S△ADF:S四边形DEGF:S四边形EBCG等于( )
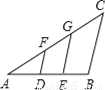
A. 1:1:1 B. 1:2:3 C. 1:4:9 D. 1:3:5
D 【解析】试题解析:∵DF∥EG∥BC, 设 ∴S四边形DEGF=S△AEG﹣S△ADF=3x,S四边形EBCG=S△ABC﹣S△AEG=5x, ∴S△ADF:S四边形DEGF:S四边形EBCG=1:3:5, 故选D.查看答案和解析>>
科目:初中数学 来源:湖北省十堰市丹江口市2018届九年级(上)期中数学试卷 题型:填空题
如图,CA,CB分别切⊙O于点A,B,D为圆上不与A,B重合的一点,已知∠ACB=58°,则∠ADB的度数为_____.
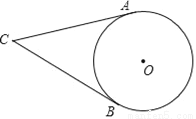
查看答案和解析>>
科目:初中数学 来源:湖北省十堰市丹江口市2018届九年级(上)期中数学试卷 题型:单选题
某中学课外兴趣活动小组准备围建一个矩形苗圃圆,其中一边靠墙,另外三边用长为40米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米,围成的苗圃面积为y,则y关于x的函数关系式为( )
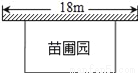
A. y=x(40﹣x) B. y=x(18﹣x) C. y=x(40﹣2x) D. y=2x(40﹣2x)
C 【解析】垂直于墙的一边的长为x米,所以平行于墙的边的长度则为(40-2x)米, 由题意则有:y=x(40-2x), 故选C.查看答案和解析>>
科目:初中数学 来源:浙江省杭州市白马湖2017-2018学年八年级上学期期中数学试卷(含解析) 题型:解答题
如图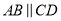 ,
, 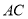 平分
平分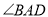 ,
, 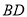 平分
平分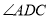 ,
, 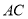 和
和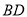 交于点
交于点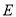 ,
, 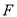 为
为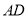 的中点,连结
的中点,连结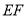 .
.
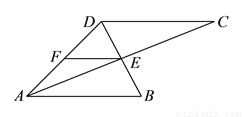
(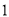 )找出图中所有的等腰三角形.
)找出图中所有的等腰三角形.
(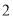 )若
)若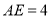 ,
, 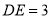 ,求
,求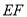 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市白马湖2017-2018学年八年级上学期期中数学试卷(含解析) 题型:填空题
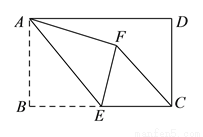
如图,在矩形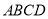 中,
中, 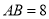 ,
, 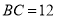 ,点
,点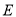 为
为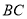 的中点,将
的中点,将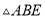 沿
沿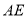 折叠,使点
折叠,使点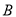 落在矩形内点
落在矩形内点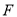 处,连接
处,连接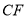 ,则
,则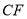 的长为__________.
的长为__________.
查看答案和解析>>
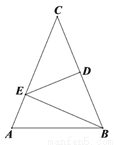
科目:初中数学 来源:广东省广州市番禺区2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
如图, 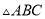 中,
中, 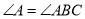 ,
, 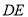 垂直平分
垂直平分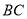 ,交
,交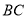 于点
于点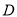 ,交
,交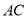 于点
于点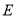 .
.
(1)若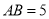 ,
, 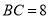 ,求
,求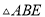 的周长;
的周长;
(2)若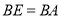 ,求
,求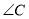 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com