下列计算正确的是( )A. x+x2=x3 B. x2•x3=x6 C. (x3)2=x6 D. x9÷x3=x3 C [解析]试题分析:根据同类项的知识.可知x+不能继续进行计算.故A不正确, 根据同底数幂相乘.底数不变.指数相加.可得.故B不正确, 根据幂的乘方.底数不变.指数相乘.可得.故C正确, 根据同底数幂相除.底数不变.指数相题目和参考答案——青夏教育精英家教网—

下列计算正确的是（　　）

A. x+x2=x3 B. x2•x3=x6 C. （x3）2=x6 D. x9÷x3=x3

C 【解析】试题分析：根据同类项的知识，可知x+不能继续进行计算，故A不正确；根据同底数幂相乘，底数不变，指数相加，可得，故B不正确；根据幂的乘方，底数不变，指数相乘，可得，故C正确；根据同底数幂相除，底数不变，指数相减，可得，故D不正确．故选C

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：北师大版七年级数学下1.4.2 单项式与多项式相乘同步练习 题型：单选题

下列计算错误的是(　　)

A. -3x(2-x)=-6x+3x2

B. (2m2n-3mn2)(-mn)=-2m3n2+3m2n3

C. xy(x2y-xy2-1)=x3y2-x2y3

D. 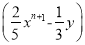xy=xn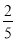+2y-xy2

C 【解析】解：A． -3x(2-x)=-6x+3x2，正确； B． (2m2n-3mn2)(-mn)=-2m3n2+3m2n3，正确； C． xy(x2y-xy2-1)=x3y2-x2y3-xy，故C错误； D． xy=xn+2y-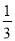xy2，正确．故选C．

查看答案和解析>>

科目：初中数学 来源：北师大版九年级上册数学全册综合测试卷一 题型：单选题

顺次连接菱形各边的中点所形成的四边形是（）

A. 等腰梯形 B. 矩形 C. 菱形 D. 正方形

B 【解析】 ∵E，F是中点， ∴EH∥BD，同理，EF∥AC，GH∥AC，FG∥BD， ∴EH∥FG，EF∥GH，则四边形EFGH是平行四边形。又∵AC⊥BD， ∴EF⊥EH， ∴平行四边形EFGH是矩形。故选：B.

查看答案和解析>>

科目：初中数学 来源：北师大版数学七年级下册同步测试 1.3 同底数幂的除法 题型：单选题

下列运算正确的是（　　）

A. （x﹣2）2=x2﹣4 B. x3•x4=x12 C. x6÷x3=x2 D. （x2）3=x6

D 【解析】选项A，原式=；选项B，原式=；选项C，原式=；选项D，原式=.故选D.

查看答案和解析>>

科目：初中数学 来源：北师大版数学七年级下册同步测试 1.3 同底数幂的除法 题型：单选题

下列运算结果为a6的是（）

A. a2+a3 B. a2•a3 C. （﹣a2）3 D. a8÷a2

D 【解析】试题分析：A、a3÷a2不能合并，故A错误；B、a2•a3=a5，故B错误；C、（﹣a2•）3=﹣a6，故C错误；D、a8÷a2=a6，故D正确；故选D．

查看答案和解析>>

科目：初中数学 来源：2017-2018学年九年级数学人教版上册：第21章一元二次方程单元测试卷 题型：解答题

关于x的一元二次方程x2＋(2k＋1)x＋k2＋1＝0有两个不等实根x1，x2.

(1)求实数k的取值范围；

(2)若方程两实根x1，x2满足|x1|＋|x2|＝x1·x2，求k的值．

(1) k＞；(2)k=2 【解析】试题分析：（1）根据根与系数的关系得出△＞0，代入求出即可；（2）根据根与系数的关系得出x1+x2=﹣（2k+1），x1•x2=k2+1，根据x1+x2=﹣x1•x2得出﹣（2k+1）=﹣（k2+1），求出方程的解，再根据（1）的范围确定即可．试题解析：（1）∵原方程有两个不相等的实数根， ∴△=（2k+1）2﹣4（k2+1）＞0， ...

查看答案和解析>>

科目：初中数学 来源：2017-2018学年九年级数学人教版上册：第21章一元二次方程单元测试卷 题型：填空题

设一元二次方程x2－3x－1＝0的两根分别是x1，x2，则x1＋x2(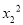－3x2)＝______.

3 【解析】一元二次方程x2－3x－1＝0的一个根是x2，即可得－3x2－1＝0，所以－3x2＝1，再由根与系数的关系可得x1＋x2＝3，所以x1＋x2(－3x2)＝3×1=3.