
设二次函数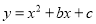 ,当
,当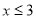 时,总有
时,总有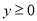 ,当
,当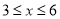 时,总有
时,总有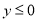 ,则
,则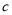 的取值范围是__________.
的取值范围是__________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:黄金30题系列 八年级数学 小题好拿分 题型:填空题
某公路急转弯处设立了一面圆型大镜子,从镜子中看到汽车车的部分号码如图所示,则该车牌照的部分号码为__________.
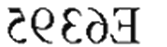
查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016-17学年度第一学期期末教学质量检测七年级数学试卷 题型:解答题
春节将至,市区两大商场均推出优惠活动:
①商场一全场购物每满100元返30元现金(不足100元不返);
②商场二所有的商品均按8折销售.
某同学在两家商场发现他看中的运动服的单价相同,书包的单价也相同,这两件商品的单价之和为470元,且运动服的单价是书包的单价的7倍少10元.
(1)根据以上信息,求运动服和书包的单价.
(2)该同学要购买这两件商品,请你帮他设计出最佳的购买方案,并求出他所要付的费用.
(1)设书包的单价为60元,运动服的单价为410元; (2)他应在商场一购买运动服,在商场二购买书包,此时所付的费用为338元. 【解析】试题分析:(1)利用运动服的单价是书包的单价的7倍少10元,可设书包单价为x元,则运动服的单价为(7x-10)元,然后根据价格和列方程,再解方程求出x和7x-10即可; (2)商场二商品八折销售,则470元的价格实际费用为470×0.8;商场一...查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016-17学年度第一学期期末教学质量检测七年级数学试卷 题型:单选题
数轴A、B两点相距4个单位长度,且A,B两点表示的数的绝对值相等,那么A、B两点表示的数是( )
A. ?4,4 B. ?2,2 C. 2,2 D. 4,0
B 【解析】∵A,B两点表示的数的绝对值相等, ∴A、B互为相反数,设A表示的数为x,则B表示的数为-x, ∴x-(-x)=4,x=2,x-=-2. 故选:B.查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
如图所示,已知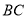 是⊙
是⊙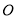 的直径,
的直径, 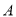 、
、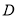 是⊙
是⊙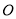 上的两点.
上的两点.

(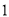 )若
)若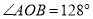 ,求
,求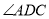 的度数.
的度数.
(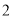 )已知
)已知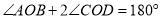 ,连接
,连接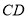 、
、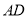 ,其中
,其中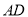 与直径
与直径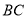 相交于点
相交于点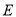 ,求证:
,求证: 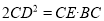 .
.
(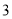 )在(
)在(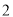 )的条件下,若
)的条件下,若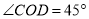 ,求
,求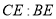 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
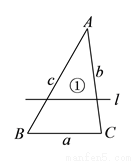
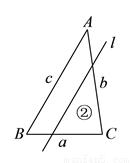
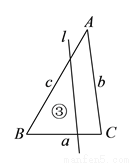
如图,已知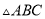 的三边长为
的三边长为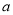 ,
, 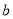 ,
, 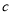 ,且
,且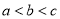 ,若平行于三角形一边的直线
,若平行于三角形一边的直线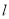 将
将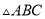 的周长分成相等的两部分,设图中的小三角形①、②、③的面积分别为
的周长分成相等的两部分,设图中的小三角形①、②、③的面积分别为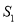 、
、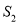 、
、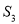 ,则
,则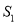 、
、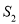 、
、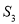 的大小关系是( ).
的大小关系是( ).
A. 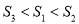 B.
B. 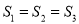 C.
C. 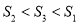 D.
D. 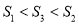
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
如图,点 、
、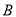 、
、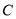 在⊙
在⊙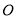 上,
上, 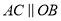 ,
, 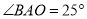 ,则
,则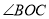 的度数为( ).
的度数为( ).

A. 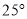 B.
B. 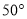 C.
C. 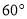 D.
D. 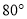
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:填空题
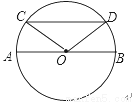
如图,在⊙O中,直径AB∥弦CD,若∠COD=120°,则∠BOD= ________.
查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年八年级上期末模拟数学试卷 题型:解答题
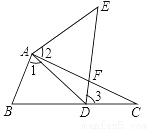
如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE,求证:AB=AD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com