练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    的倒数是（　　）

    A. 2 B. ﹣2 C. D. ﹣

    A 【解析】∵乘积为1的两个数互为倒数， ∴的倒数是2. 故选A.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：广西岑溪市2018届九年级上学期期中抽考数学试卷 题型：解答题

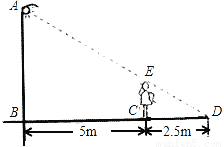
    如图所示，小华站在距离路灯的灯杆（AB）5m的C点处，测得她在路灯灯光下的影长（CD）为2.5m，已知小华的身高（EC）是1.6m，求路灯的灯杆AB的高度．

    路灯的高度AB是4.8米. 【解析】试题分析： 试题解析：先证明△ABD∽△ECD，则利用相似比得到，根据比例性质可求出AB. 依题意知：AB∥EC ， ∴ △ABD ∽ △ECD ， ∴ ， 即： ， ∴ AB＝4.8 ， 答：路灯的高度AB是4.8米.

    查看答案和解析>>

    科目：初中数学 来源：湖北省武汉市江夏区2017-2018学年八年级（上）期中数学试卷 题型：单选题

    如图，在3×3的正方形网格中由四个格点A，B，C，D，以其中一点为原点，网格线所在直线为坐标轴，建立平面直角坐标系，使其余三个点中存在两个点关于一条坐标轴对称，则原点是（　　）

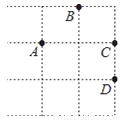
    A. A点 B. B点 C. C点 D. D点

    B 【解析】试题解析：当以点B为原点时，A（-1，-1），C（1，-1）， 则点A和点C关于y轴对称，符合条件， 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017年河北省中考数学三模试卷 题型：单选题

    任意一条线段EF，其垂直平分线的尺规作图痕迹如图所示．若连接EH、HF、FG，GE，则下列结论中，不一定正确的是（　　）

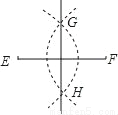
    A. △EGH为等腰三角形 B. △EGF为等边三角形

    C. 四边形EGFH为菱形 D. △EHF为等腰三角形

    B 【解析】试题分析：根据线段垂直平分线的性质可得EG=EH=FH=GF，由此可得选项A正确，选项B错误，选项C、正确，选项D正确．故答案选B．

    查看答案和解析>>

    科目：初中数学 来源：2017年河北省中考数学三模试卷 题型：单选题

    设四边形的内角和等于a，五边形的外角和等于b，则a与b的关系是（　　）

    A. a＞b B. a=b C. a＜b D. b=a+180°

    B 【解析】∵四边形的内角和等于a， ∴a=（4﹣2）•180°=360°． ∵五边形的外角和等于b， ∴b=360°， ∴a=b． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：江苏省苏州市2017-2018学年七年级上期中试卷数学试卷 题型：解答题

    解下列方程

    （）．

    （）．

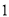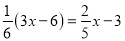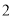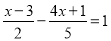    （）．（）． 【解析】试题分析：（1）方程去分母，去括号，移项合并，把x系数化为1，即可求出解； （2）方程去分母，去括号，移项合并，把x系数化为1，即可求出解． （）， ， ； （）， ， ， ．

    查看答案和解析>>

    科目：初中数学 来源：江苏省苏州市2017-2018学年七年级上期中试卷数学试卷 题型：填空题

    若|a|=8，|b|=5，且a+b＞0，那么a－b=___________.

    3或13 【解析】【解析】 ∵|a|=8，|b|=5，∴a=±8，b=±5； ∵a+b＞0，∴a=8，b=±5． 当a=8，b=5时，a﹣b=3； 当a=8，b=﹣5时，a﹣b=13； 故a﹣b的值为3或13．

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省中考数学模拟试卷 题型：解答题

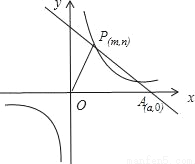
    已知：O是坐标原点，P（m，n）（m＞0）是函数y=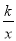（k＞0）上的点，过点P作直线PA⊥OP于P，直线PA与x轴的正半轴交于点A（a，0）（a＞m）．设△OPA的面积为s，且s=1+．

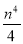    （1）当n=1时，求点A的坐标；

    （2）若OP=AP，求k的值；

    （3）设n是小于20的整数，且k≠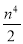，求OP2的最小值．

    （1）A（，0）；（2）2；（3）5. 【解析】试题分析：（1）根据三角形的面积公式得到 而 把代入就可以得到的值． （2）易证是等腰直角三角形，得到 根据三角形的面积 就可以解得的值． （3）易证 根据相似三角形面积的比等于相似比的平方，就可以得到关于的方程，从而求出的值．得到的值． 试题解析：过点P作PQ⊥x轴于Q，则PQ=n，OQ=m， (1)当n=1时, ...

    查看答案和解析>>

    科目：初中数学 来源：福建省2017-2018学年七年级上学期期中考试数学试卷 题型：单选题

    下列去括号错误的是（ ）

    A. 2x2﹣（x﹣3y）=2x2﹣x+3y B. 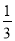x2+（3y2﹣2xy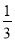）=x2﹣3y2+2xy

    C. a2+（﹣a+1）=a2﹣a+1 D. ﹣（b﹣2a）﹣（﹣a2+b2）=﹣b+2a+a2﹣b2

    B 【解析】A. ∵ 2x2﹣（x﹣3y）=2x2﹣x+3y ，故正确； B. ∵x2+（3y2﹣2xy）=x2+3y2-2xy，故不正确； C. ∵a2+（﹣a+1）=a2﹣a+1，故正确； D. ∵ ﹣（b﹣2a）﹣（﹣a2+b2）=﹣b+2a+a2﹣b2，故正确； 故选B.

    查看答案和解析>>

    同步练习册答案