
函数y=ax2-a与y=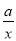 (a≠0)在同一直角坐标系中的图象可能是( )
(a≠0)在同一直角坐标系中的图象可能是( )
A. 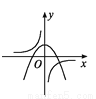 B.
B. 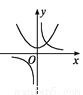 C.
C. 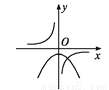 D.
D. 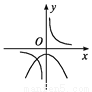
科目:初中数学 来源:湖北省大冶市金湖街办2017-2018学年八年级上学期第二次月考(12月)数学试卷 题型:单选题
如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,S△ABC=15,DE=3,AB=6,则AC的长是( )
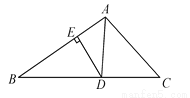
A. 7 B. 6 C. 5 D. 4
D 【解析】试题分析:∵DE=3,AB=6, ∴△ABD的面积为, ∵S△ABC=15, ∴△ADC的面积=15-9=6, ∵AD平分∠BAC,DE⊥AB于E, ∴AC边上的高=DE=3, ∴AC=6×2÷3=4, 故选D.查看答案和解析>>
科目:初中数学 来源:浙江省湖州市吴兴区2017-2018学年九年级上学期期末考试数学试卷 题型:单选题
在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.如图,已知⊙O的半径为5,则抛物线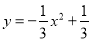 与该圆所围成的阴影部分(不包括边界)的整点个数是( )
与该圆所围成的阴影部分(不包括边界)的整点个数是( )
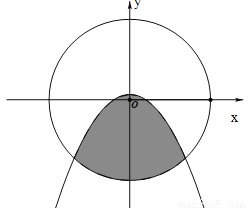
A. 24 B. 23 C. 22 D. 21
D 【解析】∵抛物线顶点坐标为(0, ), 半径为5的⊙O与y轴负半轴交点为(0,-5), ∴当y=0时,x=±1,∴整点为(1,0),(0,0),(-1,0); 当y=-1,x=±2,∴整点为(2,-1),(-1,-1),(0,-1),(1,-1),(2,-1); 当y=-2,x=±,∴整点为(2,-2),(-1,-2),(0,-2),(1,-2),(2,-2); ...查看答案和解析>>
科目:初中数学 来源:2018春季学北师大版九年级数学下册期末测评试卷 题型:填空题
如图,已知点A从点(1,0)出发,以每秒1个单位长度的速度沿着x轴的正方向运动,经过t s后,以O,A为顶点作菱形OABC,使点B,C都在第一象限内,且∠AOC=60°,又以点P(0,4)为圆心,PC为半径的圆恰好与OA所在的直线相切,则t=_____.
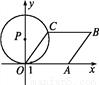
查看答案和解析>>
科目:初中数学 来源:2018春季学北师大版九年级数学下册期末测评试卷 题型:单选题
如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”.则半径为2的“等边扇形”的面积为( )
A. π B. 1 C. 2 D. 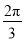
查看答案和解析>>
科目:初中数学 来源:宁夏2017-2018学年度上期七年级数学期末综合检测模拟试卷 题型:解答题
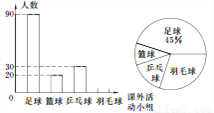
为了了解学生对体育活动的喜爱情况,某校对参加足球、篮球、乒乓球、羽毛球这四个课外活动小组的人员分布情况进行抽样调查,并根据收集的数据绘制了下面两幅不完整的统计图,请根据图中提供信息,解答下面问题.
(1)此次共调查了多少名同学?
(2)将条形统计图补充完整,并计算扇形统计图中的篮球部分的圆心角的度数;
(3)如果该校共有1000名学生参加这四个课外活动小组,而每个教师最多只能辅导本组20名学生,请通过计算确定每个课外活动小组至少需要准备多少名教师.
查看答案和解析>>
科目:初中数学 来源:宁夏2017-2018学年度上期七年级数学期末综合检测模拟试卷 题型:填空题
已知三角形的第一边长是a+2b,第二边比第一边长(b - 2),第三边比第二边短5,则三角形的周长为__.
3a+8b – 9 【解析】试题解析:三角形的周长为a+2b+a+2b+b-2+a+2b+b-2-5=3a+8b-9. 故答案为:3a+8b-9.查看答案和解析>>
科目:初中数学 来源:吉林省2018届九年级(上)期中数学试卷 题型:解答题
心理学家研究发现,一般情况下,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力y随时间t(分钟)的变化规律有如下关系式:  (y值越大表示接受能力越强)
(y值越大表示接受能力越强)
(1)讲课开始后第5分钟时与讲课开始后第25分钟时比较,何时学生的注意力更集中;
(2)讲课开始后多少分钟,学生的注意力最集中能持续多少分钟;
(3)一道数学难题,需要讲解24分钟,为了效果较好,要求学生的注意力最低达到180,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
(1)讲课开始后第25分钟时学生的注意力比讲课开始后第5分钟时更集中;(2)讲课开始后10分钟时,学生的注意力最集中,能持续10分钟;(3)老师可以经过适当安排,能在学生注意力达到所需的状态下讲解完这道题目. 【解析】试题分析: (1)把t=5和t=25分别代入对应的函数关系式求出y的值,并比较大小即可得出结论; (2)由自变量的取值范围分别求出第一段函数和第三段函数中函数值取最...查看答案和解析>>
科目:初中数学 来源:2017年四川省数学七年级(上)期末数学试卷 题型:单选题
已知a+b=0,a≠b,则化简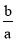 (a+1)+
(a+1)+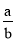 (b+1)得( )
(b+1)得( )
A. 2a B. 2b C. 2 D. -2
D 【解析】试题解析: (a+1)+ (b+1), =b++a+, =(a+b)+(+), 又∵a+b=0,a≠b, ∴a=-b, ∴==-1, ∴ (a+1)+ (b+1), =(a+b)+(+), =-2. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com