
有五张反面相同的卡片的正面分别写有“我”“的”“中”“国”“梦”,五张卡片洗匀后将其反面朝上放在桌面上,小明从中任意抽取两张卡片,恰好是“中国”的概率是( )
A. 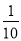 B.
B. 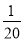 C.
C. 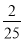 D.
D. 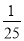
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:北师大版七年级数学下册 第二章 相交线与平行线 2.2 探索直线平行的条件 同位角及平行公理 同步课堂练习题 题型:单选题
如图,直线AB、CD被直线EF所截,则∠AMN的同位角是( )
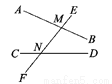
A. ∠CNM B. ∠CNF C. ∠DNF D. ∠DNM
B 【解析】∵直线AB、CD被直线EF所截, ∴只有∠AMN与∠CNF在截线EF的同侧,且在AB和CD的同旁, 即∠CNF是∠AMN的同位角。 故选B.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下2.2.1 用“同位角、第三直线”判定平行线 同步练习 题型:单选题
如图,直线a,b被直线c所截,下列条件能使a//b的是 ( )
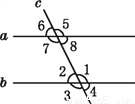
A. ∠1=∠6 B. ∠2=∠6 C. ∠1=∠3 D. ∠5=∠7
B 【解析】试题分析:利用平行线的判定方法判断即可.∵∠2=∠6(已知),∴a∥b(同位角相等,两直线平行), 则能使a∥b的条件是∠2=∠6查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷1 题型:填空题
从甲、乙2名医生和丙、丁2名护士中任意抽取2人参加医疗队,那么抽取的2人恰好是一名医生和一名护士的概率为________.
【解析】【解析】 画树状图为: 共有12种等可能的结果数,其中恰好是一名医生和一名护士的结果数为8,所以恰好是一名医生和一名护士的概率==.故答案为: .查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷1 题型:单选题
如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )
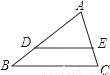
A. 1 B. 2 C. 3 D. 4
B 【解析】试题分析:根据平行线分线段成比例可得,代入计算可得: ,即可解EC=2, 故选:B.查看答案和解析>>
科目:初中数学 来源:江苏省张家港市2017-2018学年第一学期初三数学期末考试试卷 题型:解答题
如图,在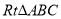 中,
中, 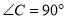 ,点
,点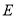 在斜边
在斜边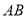 上,以
上,以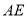 为直径的⊙
为直径的⊙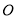 与
与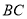 相切于
相切于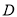 .若
.若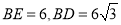 .
.
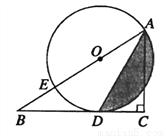
(1)求⊙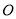 的半径;
的半径;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源:江苏省张家港市2017-2018学年第一学期初三数学期末考试试卷 题型:填空题
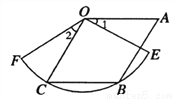
如图,四边形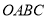 为菱形,点
为菱形,点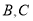 在以点
在以点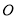 为圆心的
为圆心的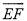 上,若
上,若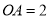 cm,
cm, 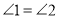 ,
,
则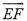 的长为_______.
的长为_______.
查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:期中检测卷 题型:解答题
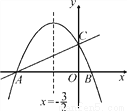
如图,在平面直角坐标系xOy中,直线y=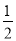 x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是直线x=-
x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是直线x=-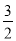 ,且经过A,C两点,与x轴的另一交点为点B.
,且经过A,C两点,与x轴的另一交点为点B.
(1)①直接写出点B的坐标;②求抛物线的解析式.
(2)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A,M,N为顶点的三角形与△ABC相似?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册数学 第二章 相交线与平行线 单元检测卷 题型:单选题
如图所示,在三角形ABC中,点D是边AB上的一点.已知∠ACB=90°,∠CDB=90°,则图中与∠A互余的角的个数是( )
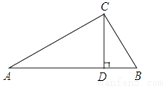
A. 1 B. 2 C. 3 D. 4
B 【解析】根据图形和余角的概念即可解答. 【解析】 ∵∠ACB=90°, ∴∠A+∠B=90°, ∵∠CDB=90°, ∴∠A+∠ACD=90°, ∴与∠A互余的角有两个. 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com